Уравнение движения материальной точки
Механика твердого тела
Чтобы иметь возможность описать движение тела в математических терминах, мы должны сначала понять тип движения, которому оно подвергается. Используемый вид уравнения движения материальной точки будет варьироваться в зависимости от рассматриваемой ситуации.
Линейное движение
Существует три общих случая линейного движения, характеризующихся типом ускорения, которому оно подвергается. Виды линейного движения:
• прямолинейное равномерное;
• равноускоренное;
• переменное ускорение;
Если положение объекта изменяется по отношению к контрольной точке, то считается, что он находится в движении. Если точка не изменяется, то она находится в состоянии покоя. Для лучшего понимания или для решения различных ситуаций покоя и движения мы выводим некоторые стандартные уравнения, связывающие термины: расстояние, перемещение, скорость материальной точки уравнения движения и ускорение тела с помощью уравнений, называемых — уравнениями движения.
Прямолинейное равномерное движение
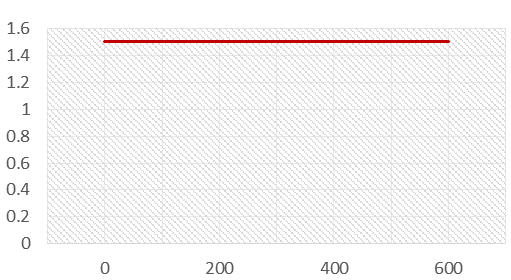
Если скорость объекта постоянно фиксирована, то объект не испытывает никакого ускорения или замедления. Его скорость будет оставаться постоянной с течением времени. На него могут действовать или не действовать силы, но нет чистой силы, заставляющей его ускоряться.
Уравнение движения, используемое в этом случае, простое, в виде:
\[v=\frac{s}{t}\]
Где: v: скорость (в м/с), s: пройденное расстояние или перемещение (в метрах), t: время, необходимое для прохождения этого расстояния (в секундах).
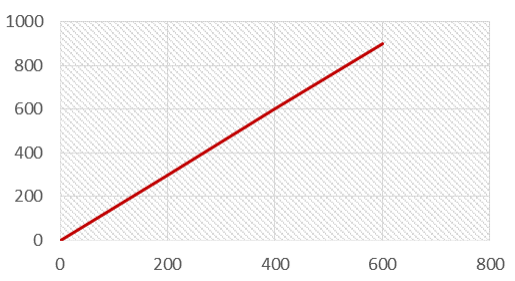
Пример 1. Человеку требуется 10 минут, чтобы дойти от точки А до точки Б. Вычислите расстояние, разделяющее две точки, предполагая, что он все время идет с постоянной скоростью 1,5 м/с.
Ответ: Во-первых, затраченное время необходимо перевести в секунды, чтобы оно соответствовало единицам измерения. Включив значения в уравнение, мы получим расстояние 900 м.
Равноускоренное движение
В этом случае тело ускоряется с постоянной скоростью на протяжении всего своего движения. Поэтому скорость, с которой оно движется, будет меняться с течением времени.
Типичные графики для этого типа движения приведены ниже.
В случае движения с равномерным или постоянным ускорением (с одинаковым изменением скорости за равный промежуток времени) мы выводим три стандартных уравнения движения, которые также известны как законы постоянного ускорения. Эти уравнения содержат величины перемещения(s), скорости (начальной и конечной), времени(t) и ускорения(a), которые управляют движением тела. Уравнения могут быть применены только в том случае, когда ускорение тела постоянно, а движение является прямой линией.
v: конечная скорость (м/с)
u: начальная скорость (м/с)
a: скорость ускорения. Если тело замедляется, то используйте знак минус (м/с2)
t: затраченное время (c)
s: пройденное расстояние (м)
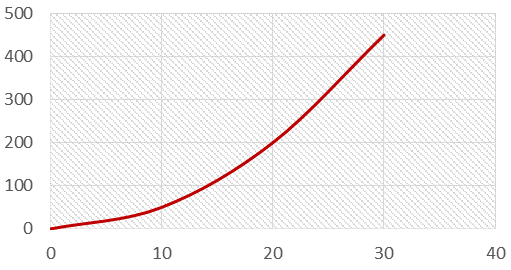
Пример 2. Объект удерживается в состоянии покоя на высоте 12 м над землей. Объект освобождается вовремя t = 0с и свободно падает под действием силы тяжести. Учитывая, что ускорение под действием силы тяжести составляет \[9,81 \mathrm{м} / \mathrm{c}^{2}\], найдите его скорость на полпути между начальной точкой и землей.
Ответ: Используем третью формулу движения \[\left(v^{2}=u^{2}+2 a c\right) \text { при } \mathrm{a}=9,81 \mathrm{~m} / \mathrm{c}^{2}, \mathrm{~s}=6 \mathrm{M}, \mathrm{u}=0 \mathrm{~m} / \mathrm{c}\]; затем мы получаем ответ 10,85 м/с.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Переменное ускорение
Каждый объект, подвергающийся этому типу движения, будет иметь определенное уравнение, описывающее его перемещение, скорость и ускорение в определенные моменты времени. Зная одно из этих уравнений, можно определить другие, интегрируя или дифференцируя их по времени. Для этого типа движения важно иметь в виду следующее:
Скорость (v) — скорость изменения расстояния (s) со временем (t) или в терминах исчисления: \[\frac{d s}{d t}\].
Ускорение (a) — это скорость изменения скорости (v) со временем (t) или в терминах исчисления: \[\frac{d^{2} s}{d t^{2}}\].
Пример 3. Тело движется в пространстве со скоростью, заданной уравнением \[v=4 t^{2}+6\]. Найдите его скорость, пройденное расстояние и ускорение за время t = 5 с.
Ответ: Скорость можно легко найти, включив t = 5 с в приведенное выше уравнение, что дает v = 506 м/с. Ускорение также можно найти, дифференцируя v и используя t = 5 с. Чтобы определить пройденное расстояние, нам нужно интегрировать v используя пределы t = 0 с и t = 5 с.
Движение по окружности
Рассмотрим тело, которое движется по окружности вокруг точки O, как показано ниже.
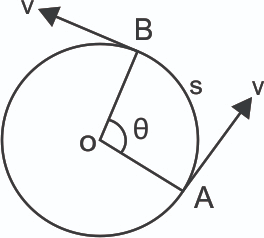
Если телу потребуется время t чтобы сделать угол θ в точке O, то мы можем найти ее угловую скорость, используя:
Период T для завершения объектом полного оборота задается формулой:
Пройденное расстояние s рассчитывается:
Линейную скорость также можно найти, разделив последнее уравнение на затраченное время t:
Чтобы тело оставалось в круговом движении, необходима сила, притягивающая его к центру. В противном случае объект сойдет с орбиты по прямой линии в соответствии с Первым законом Ньютона. Эта сила также известна как центростремительная сила, и она вызывает ускорение тела. Направление ускорения направлено к центру, которое совпадает с направлением центростремительной силы. Центростремительное ускорение может быть рассчитано как:
Движение снаряда
Рассмотрим движение снаряда, брошенного под углом x. Градусы относительно земли показаны ниже.
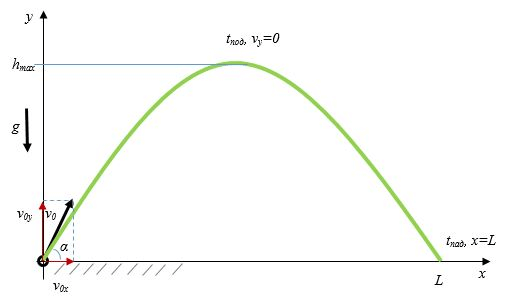
Вектор скорости u может быть разложен на 2 компонента \[u_{x} \text { и } u_{y} .\]
Как только снаряд будет выпущен, его траектория будет зависеть от двух вещей: его начальной скорости и ускорения, вызванного гравитацией.