
Расстояние между скрещивающимися прямыми, способы его нахождения, примеры, доказательства
Напомним, что скрещивающимися прямыми называют прямые, не принадлежащие одной плоскости и не имеющие между собой общих точек.
Признак скрещивания прямых: если прямая a пересекается с плоскостью, в которой лежит прямая b и при этом точка пересечения не принадлежит a, то a и b скрещиваются.
В качестве наглядного представления скрещивающихся прямых можно привести транспортную развязку. Верхнюю из дорог следует считать за одну прямую, нижнюю принять за другую.
Пусть мы имеем две скрещивающиеся в пространстве прямые. Через каждую из них можно провести плоскость, параллельную другой скрещивающейся прямой, причём только одну.
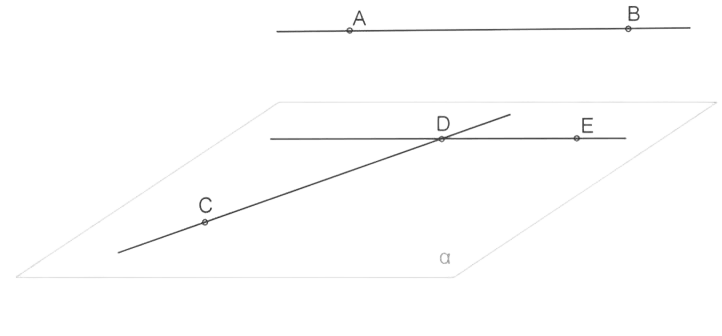
Доказательство:
Через точку D у нас получится провести прямую DE, которая будет параллельной AB.
Через CD и DE (смотрите рис. выше) можно провести плоскость α.
В связи с тем, что AB не принадлежит этой плоскости и при этом параллельна DE, то она будет параллельной и плоскости.
Указанная плоскость единственная. Это ясно из того, что любая другая плоскость, которая проходит через CD, неизбежно пересечёт DE и AB, которая ей параллельна.
Доказательство завершено.
Различные определения расстояния между скрещивающимися прямыми
Расстоянием между скрещивающимися в пространстве прямыми именуют длину промежутка, отделяющего одну из скрещивающихся прямых от параллельной плоскости, которая пересекает другую прямую.
Расстоянием между скрещивающимися прямыми это расстояние между самыми близкими точками этих прямых.
Расстоянием между двумя скрещивающимися прямыми называют расстояние, разделяющее две плоскости, которым они принадлежат.
Расстоянием между двумя скрещивающимися прямыми считают длину, которую имеет их общий перпендикуляр.
Пусть нам даны скрещивающиеся прямые a и b. Произвольно выберем на a некоторую точку M1. На b наложим плоскость χ, которая будет параллельна a. Из точки M1 на указанную плоскость χ проведём перпендикуляр M1H1. Его длина и есть расстояние, разделяющее скрещивающиеся прямые.
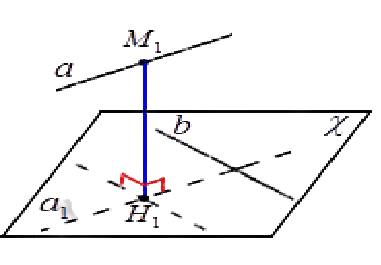
Ка найти расстояние между скрещивающимися прямыми
Главная трудность здесь состоит в построении отрезка равного по своей длине расстоянию, которое нам требуется найти. Если его удалось построить, то используя теорему Пифагора, признаки подобия или равенства треугольников либо иные подобные пути, расстояние получится найти достаточно легко.
Как следует искать расстояние между скрещивающимися прямыми методом координат
Он основан на определении 5 и использовании формулы расстояния от точки M до плоскости α.
r(M, a) = (ax0 + by0 + cz0 + d)/ √(a2 + b2 + c2)
Последовательность действий здесь следующая:
- Выясняем, какие координаты имеют точки M1 (x1, y1, z1)и M2(x2, y2,z2) , принадлежащие прямым a и b;
- Выясняем координаты (ax,ay,az) и (bx,by,bz), принадлежащие направляющим векторам a и b;
- Выясняем, какие координаты (A,B,C) имеет нормальный вектор n плоскости χ, который проходит через b, параллельной a. Проще всего это сделать из равенства
- Записываем общее уравнение плоскости χ как
\[\mathrm{A}\left(\mathrm{x}-\mathrm{x}_{1}\right)+\mathrm{B}\left(\mathrm{y}-\mathrm{y}_{1}\right)+\mathrm{C}\left(\mathrm{z}-\mathrm{z}_{1}\right)=0;\] - Приводим полученное уравнение к нормальному виду
\[\cos \alpha * \mathrm{x}+\cos \beta * \mathrm{y}+\cos \gamma * \mathrm{z}-\mathrm{p}=0;\] - Вычисляем величину промежутка M1H1 от точки M(x1,y1,z1) до плоскости χ по формуле
В системе координат заданы скрещивающиеся прямые a и b.
Первая определена параметрическими уравнениями \[\mathrm{x}=-2, \mathrm{y}=1+2 * \lambda, \mathrm{z}=4-3^{*} \lambda\]
Вторая задана каноническим уравнением \[\mathrm{x} / 1=(\mathrm{y}-1) /-2=(\mathrm{z}+4) / 6\]
Нужно выяснить расстояние между этими прямыми.
Решение: Из уравнений прямых ясно, что первая из них проходит через точку M1(-2, 1,4), а вторая через точку M2(0,1,-4).
Направляющий вектор первой прямой a = (0,2,-3). Второй – b = (1,-2,6).
Вычислим векторное произведение указанных векторов.
\[\mathrm{n}=\left[\begin{array}{llcc}
a \mathrm{X} b
\end{array}\right]=\begin{array}{ccc}
i & j & k \\
0 & 2 & -3 \\
1 & -2 & 6
\end{array}=6 * I-3* \mathrm{j}-2* \mathrm{k}\]
У n будут координаты (6, -3, -2).
Из этого получается, что уравнение плоскости χ является уравнением той плоскости, которой принадлежит точка M2(0,1,-4). Она имеет нормальный вектор n = (6,-3,-2).
6*(x-0) — 3(y-1) – 2(z-(-4)) = 0
6x – 3y – 2z – 5 = 0
Нормирующим множителем выше указанного уравнения плоскости будет
1/ √((62) – (-3)2 – (-22)) = 1/7
Отсюда следует, что у уравнения данной плоскости будет вид
(6/7)*x – (3/7)*y – (2/7)*z – 5/7 = 0
Теперь нам осталось лишь воспользоваться формулой расстояния от точки M1(-2,1,4) до плоскости (6/7)*x – (3/7)*y – (2/7)*z – 5/7 = 0
В результате несложных вычислений мы получаем
M1H1= ((6/7)*(-2) – (3/7)*1 – (2/7)*4 – (5/7) = (-28/7) = 4
Ответ: расстояние между прямыми равно 4.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Метод базирующийся на определении 1
Его покажем сразу на решении конкретно задачи. Так будет понятнее и яснее.
Основанием прямоугольной призмы АВСDA1B1C1D1 является квадрат ABCD. Каждая из его сторон равна 4. Высота призмы 2√2. Требуется найти величину промежутка между прямыми DA1 и CD1.
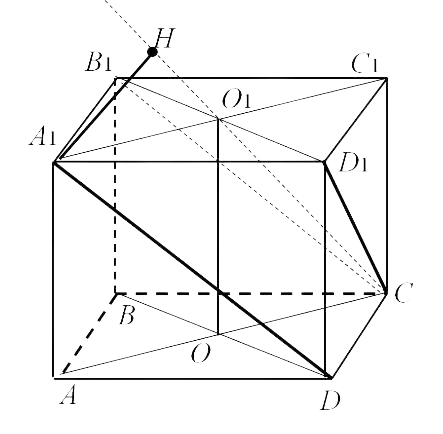
Решение: Т. к. прямая CD1 принадлежит плоскости CB1D1 . DA1||CB1, прямая DA1 является параллельной плоскости CB1D1. Из сказанного следует, что нужно найти разделяющее их расстояние. Оно и будет ответом на наш вопрос. Упомянутое расстояние, есть расстояние от точки A1 до плоскости CB1D1.
BD1 перпендикулярна плоскости ACC1. Из этого следует, что плоскость ACC1 будет перпендикулярной плоскости CB1D1. Их пересечением является прямая O1C. O и O1 есть центры верхнего и нижнего оснований призмы.
Из точки A1, которая принадлежит плоскости ACC1 опустим перпендикуляр A1H на прямую CO1. Длина A1H будет тем расстоянием, которое мы ищем.
Из прямоугольного треугольника A1HO1, зная, что его гипотенуза AO1 равна 2√2, и
sin(HO1A1) = √2/2 находим катет HA1 = A1O1sin(HO1A1) = 2.
Ответ: величина промежутка между прямыми DA1 и CD1 равно 2.
Метод объёмов
Он использует вспомогательную пирамиду, высота которой и будет искомым расстоянием, разделяющем скрещивающиеся прямые. Для нахождения упомянутой высоты сначала нужно узнать объём указанной пирамиды. Отсюда и название метода.
Отметим, что данный метод исключает проведение перпендикуляра к скрещивающимся прямым.
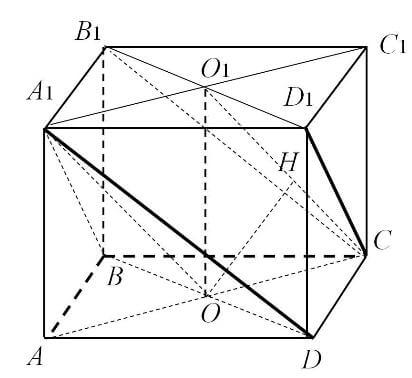
Выясните, чему равна величина промежутка между прямыми A1D и D1C. Сторона квадрата равна 4. Высота призмы 2√2.
Решение: Т. к. DA1||CB1 и CD1||BA1 , то (BDA1 )||(CB1D1). Расстояние между указанными плоскостями равняется расстоянию от точки C до плоскости A1BD.
Посмотрите на пирамиду BCDA1. H – высота, соединяющая вершину С с основанием BDA1.
Длина высоты равняется расстоянию между DA1 и DC1.
BD = AC = √32 = 4√2. AO = 2√2
Из прямоугольного треугольника легко находим
A1O = CO1 = √(AA12 + AO2) = √(4*2 + 4*2) = 4
Находим объём пирамиды CA1BD. Она имеет основание A1BD и высоту h. Он будет равен
V(1) = (1/3)SABD * h = (1/3)*(1/2)A1O * BD * h = (4 * 4√2)*h/6 = (8√2)*h/3
Вычислим теперь той же самой пирамиды объём, считая её основанием BCD, а высоту AA1.
V{2} = (1/3)SBCD*AA1 = (1/3)*(1/2)*16*2√2 = 16*(√2/3)
Теперь приравняем эти выражения
[(8√2)*h/3] = [16*(√2/3)]
Из этого выражения очень легко найти расстояние между прямыми DA1 и CD1. Упрощаем и получаем, что h = 2.
Ответ: величина промежутка равна 2.










