Понятие электрического поля
Понятие электрического поля
Электрическое поле — это особый вид материи, которая существует вокруг каждой заряженной частицы и оказывает силовое воздействие на соседние частицы (притягивает их либо отталкивает). Другими словами, электрическое поле частицы позволяет ей взаимодействовать с другими частицами без непосредственного соприкосновения с ними. Электрическое поле оказывает заметное силовое воздействие только вблизи частицы, из которого оно исходит.
Благодаря взаимной компенсации встречных силовых воздействий всех электрополей, сгруппированные частицы обычно пребывают в относительном покое (электрическая нейтральность). Когда же подобное равновесие нарушается, между электрополями частиц начинается перераспределение их воздействий, что образует положительный или отрицательный электрический заряд (q).
Самый яркий пример такого перераспределения — это включение любого электроприбора через вилку в розетку. Электричество (движение зарядов) возникает в электроприборе только после физического приближения его уравновешенной системы к нестабильной системе частиц электросети. Источником же нестабильности в проводах электросети является воздействие на нее других неуравновешенных систем: поток воды, ветер, сжигание топлива, управляемая ядерная энергия и т.д. Все типы электрогенераторов используют природное либо искусственное движение в пространстве большого количества частиц. С помощью этого движения в проводе-проводнике поддерживается неуравновешенность электрополей его частиц.
Понятие электростатического поля
Электростатическое поле является разновидностью электрического поля, и обладает следующими характеристиками:
- Его электрические заряды неподвижны в пространстве поля.
- При отсутствии в системе электрических токов, электрические заряды остаются неизменными.
- Силовые линии поля незамкнуты, не пересекаются и не касаются друг друга.
- С увеличением напряженности поля возрастает густота его силовых линий.
- При перемещении заряда внутри поля его траектория не имеет значения. При расчетах учитывается только величина заряда, а также координаты начальной и конечной точки.
По своим свойствам электростатическое поле схоже с гравитационным. При рассмотрении кулоновских и гравитационных сил в физике применяются одни и те же соотношения, что и образует их схожесть.
Понятие потенциала электрического поля
Уравновешенная система заряженных частиц не способна самостоятельно совершать работу из-за взаимной компенсации своих электрических полей. Однако каждое электрически нейтральное тело обладает возможностью совершить работу при внесении нестабильности в структуру полей его частиц.
Величина энергии, которую можно извлечь из уравновешенных электрических полей частиц, называется потенциалом электрического поля (φ). Иными словами, потенциал является скалярной энергетической характеристикой электрополя. Рассчитывают подобный потенциал (φ) путем деления величины потенциальной энергии электрического заряда (Wp) на величину этого заряда (q):
Единицей измерения потенциала электрического поля является вольт (В), который определяет разность потенциалов между двумя точками, для перемещения через которые заряду величиной в 1 кулон (Кл) потребуется работа величиной в 1 джоуль (Дж). Исходя из этого, рассчитать работу (А) совершаемую зарядом при перемещении, можно по следующей формуле:
Расчетная же формула единицы измерения потенциала поля выглядит следующим образом:
Для обозначения разности потенциалов поля в формулах принято применять символ Δφ.
Особенности потенциала электростатического поля
Допустим, точечный электрический заряд, пребывая в некой точке пространства, образует именно электростатический тип электрического поля. В этом случае потенциал подобного поля будет равен величине работы, которая потребуется электрическим силам для перемещения единичного положительного заряда из исходной (нулевой) точки на бесконечно далекое расстояние:
С помощью такого математического решения снимается проблема с определением потенциала этого уникального типа поля с его неподвижными и неизменяемыми зарядами. Принимая при расчетах условный факт бесконечного расстояния (r) между начальной и конечной точкой, вычислить потенциал точечного заряда уже можно по следующей формуле:
Если, исходя из теоремы Гаусса, принять что r ≥ R, то с помощью данной формулы можно вычислить потенциал электростатического поля однородно заряженной шара либо сферы.
Работа сил в электрическом поле
Наглядно увидеть работу электрических сил в электрополе можно с помощью пробного заряда q. Благодаря ему формулу работы для малого перемещения можно вывести следующим образом:
Графически подобная работа в электрическом поле будет выглядеть так:
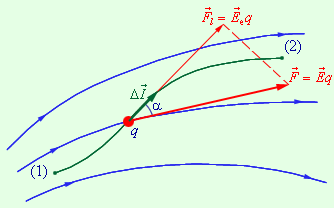
Чтобы определить силу воздействия электрического поля на заряженную частицу или тело, в электродинамике была введена векторная величина (Е) получившая название «напряженность»:
Напряженность Е измеряет интенсивность поля. При этом направление напряженности совпадает с направлением силы, действующей на положительно заряженную частицу.
Сама же работа (А), которую внутри себя совершает электрополе для перемещения заряда из точки в точку, называется «электрическим напряжением» (U).

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Работа сил электростатического поля
Характеристики электростатического типа электрополя накладывают свои особенности при расчете его работы по перемещении заряда. В связи с тем, что форма траектории заряда не имеет значения, логично предполагать, что в электростатическом поле, при перемещении заряда по любой замкнутой траектории, работа сил поля будет равна нулю.
Рассмотрим данное предположение на примере работы кулоновских сил для двух различных траекторий пробного заряда q в электрополе, образованном благодаря заряду Q. Малое перемещение на одной из траекторий обозначим символом \[\Delta \vec{l}\]. Теперь выведем формулу кулоновских сил в электрополе:
Из формулы становится понятно, что зависимость ее результата привязана к работе, к расстоянию между зарядом-источником поля и перемещаемого заряда, а также к изменению этого расстояния. Если проинтегрировать данное выражение на интервале от r = r1 до r = r2, то получаем следующую формулу работы сил электростатического поля:
Теперь изобразим графически работу кулоновских сил при двух перемещениях заряда из точки в точку с разной формой траектории:
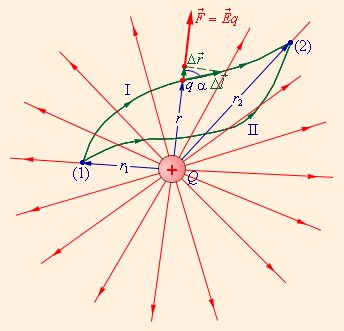
Как видим, при обоих перемещениях кулоновские силы произвели одну и ту же работу, ведь при расчете учитываются только координаты начальной и конечной точки, а не то, какой путь между ними проделал заряд.
Далее, если мы изменим вектор движения заряда на противоположный, то и работа тоже поменяет знак. В случае же, когда заряд будет перемещаться по замкнутой траектории (кружить), то, следуя формуле, работа примет нулевое значение. Любое поле, обладающее свойством не иметь работы при замкнутом кружении частицы, называется потенциальным или, по другому, консервативным.
Таким необычным поведением на микроуровне заряженные частицы обязаны особенностями структуры электростатического поля. Согласно главной характеристике подобного поля, оно представляет собой сочетание распределенных и неизменяемых точечных зарядов. И по известному принципу суперпозиции, при перемещении пробного (стороннего) заряда, работа результирующего поля будет равна сумме работ кулоновских полей всех тех зарядов, которые как раз и являются источником их общего электростатического поля.
Существует также иной способ вычислить работу электростатического поля при перемещении в нем заряда. Для этого необходимо рассмотреть свойство потенциальности поля и применить в расчетах потенциальную энергию заряда в электрополе.
Согласно базовому определению, работа электростатического поля, которую оно совершает для перемещения заряда из любой точки своего пространства в нулевую точку, равна потенциальной энергии этого заряда.
Допустим, мы выберем какую-нибудь точку в пространстве координат электростатического поля, поместим в это место заряд и присвоим ее потенциальной энергии нулевое значение (0).
Далее, чтобы не перепутать потенциальную энергию с напряжением поля, обозначаем энергию не как «Е», а как «W». Работу же электрополя обозначаем как «A10».В результате получаем следующую формулу:
Сама по себе величина потенциальной энергии заряда в электростатическом поле смысла не имеет, так как уже неоднократно сказано выше, важны лишь значения координат начальной и конечной точек перемещения. Однако математически потенциальную энергию заряда можно успешно использовать для вычисления совершаемой полем работы. Для этого надо всего лишь найти разность потенциальной энергии точечного заряда в первоначальной точке и в конечной:
Как видно из формулы, у помещенного в электростатическое поле заряда q его потенциальная энергия прямо пропорциональна его величине.
Изображение электрического поля через эквипотенциальные поверхности
Для лучшего понимания структуры электростатического поля, кроме графиков с силовыми линиями применяется также и его отображение через эквипотенциальные поверхности. Подобные поверхности иначе еще называют поверхностями равного потенциала. Они обладают следующими важными свойствами:
- На эквипотенциальной поверхности у всех ее точек потенциал электрического поля принимает одно и то же значение. То есть, потенциал всех поверхностных точек одинаков.
- На графических изображениях силовые линии поля всегда перпендикулярны эквипотенциальным поверхностям.
- При условии однородности электрополя, его эквипотенциальные поверхности выстраиваются параллельно друг другу, то есть являются параллельными плоскостями.
На простом изображении точечного заряда в кулоновском поле эквипотенциальные поверхности принимают вид концентрических сфер. Структуры же взаимодействующих друг с другом полей образуют уже более сложные графические узоры.
На трех рисунках ниже синие окружности отображают эквипотенциальные поверхности, а красным цветом обозначены силовые линии.
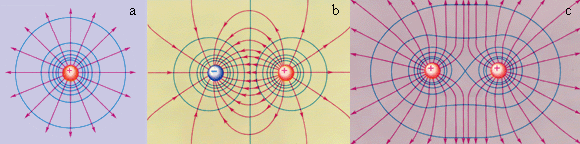
Зная свойства однородных полей и применяя к ним принцип суперпозиции напряженности полей разрядов, мы можем вывести и суперпозицию для потенциалов:
φ = φ 1 + φ 2 + φ 3 + . . .
Но перед этим необходимо установить взаимосвязь между потенциалом поля и его напряженностью. Данная закономерность находится при вычислении работы малого перемещения пробного заряда q из точки 1 в конечную точку 2 вдоль силовой линии (координату, которую следует отсчитывать вдоль силовой линии, обозначаем буквой l):
Исходя из того, что изменение потенциала определено как \[\Delta \varphi=\varphi_{1}-\varphi_{2}\], выводим напряженность поля:
В последнем выражении связь между потенциалом и напряжением уже становится очевидной.














