Электродвижущая сила (ЭДС)
Неотъемлемым элементом любой самодостаточной электрической цепи является источник (генератор) тока. Он разделяет электрические заряды, благодаря чему напряжение поддерживается в приемлемом диапазоне значений. Без этого электрический ток с точно заданными характеристиками в цепи существовать не может. Если мы поставим в цепь, например, конденсатор (пусть даже очень ёмкий), ток в ней возникнет, но через некоторое, как правило, очень непродолжительное время, он закончится. Электрическое поле переместит все имеющиеся свободные заряды, и конденсатор разрядится.
Электродвижущая сила
Электродвижущей силой источника тока называют силы не электростатического происхождения, действующие внутри указанных устройств и перемещающие электрические заряды против электростатического поля, которое создаёт необходимую разность потенциалов.
Природа у электродвижущих сил может быть самой разной. В гальванических источниках электрического тока они возникают благодаря энергии, высвобождающейся в химических реакциях между веществом электродов и электролитов. В генераторах постоянного тока они создаются энергией магнитного поля и механической энергией вращения якоря.
Формула расчета ЭДС в электрических цепях, состоящих из замкнутых контуров
Работа электростатических сил равна нулю, ведь заряды (электроны) приходят практически в то же место откуда вышли. Не равна нулю только результирующая работа электродвижущих сил цепи.
Её величина определяется формулой электродвижущей силы:
Формула ЭДС:
\[\varepsilon=\frac{A}{q}\].
Именно этому равна электродвижущая сила. A – работа сторонних сил, т. е. ЭДС.
Обратите внимание, направлением ЭДС считается направление, в котором внутри источника перемещаются именно положительные заряды. Часто оно противоположно направлению перемещения реальных носителей заряда, в качестве которых в подавляющем большинстве случаев выполняют электроны.
Если источник тока только один, то направление ЭДС в цепи такое же, как у него.
Размерность электродвижущей силы не равна размерности силы или работы. В системе СИ величина ЭДС измеряется в вольтах. Это мера разности потенциалов, которая создаётся на зажимах при разомкнутом генераторе.
Электродвижущая сила цепи и напряжение
Представим электрическое поле. Рассмотрим в нём произвольную кривую, соединяющую между собой точки A и B. Для дальнейшего объяснения на выбранной линии следует указать положительное направление.
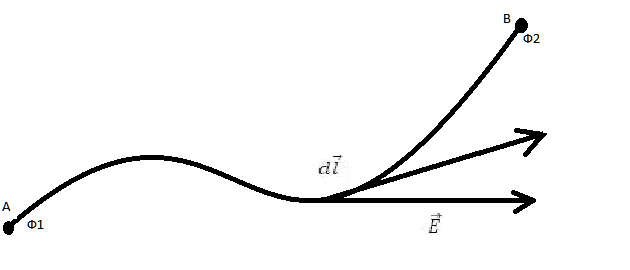
Напряжение на этой кривой будет равняться:
\[U=\int_{l} E d l\]
Под напряжённостью поля, как известно, понимают силу, действующую на помещённый в него единичный положительный заряд. Интеграл в данном случае – работа по перемещению заряда по кривой.
Значение напряжения станет равно разности потенциалов на концах нашей линии: U = φ1 – φ2.
Какую форму имеет кривая, совершенно безразлично. Важны лишь её начальные и конечные точки.
Давайте подробнее изучим циркуляцию вектора напряжённости по замкнутому контуру L.
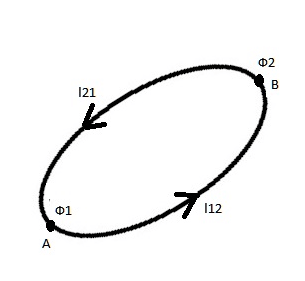
Выделим на указанном контуре точки A и B. Они разделят его на два криволинейных незамкнутых отрезка. Учитывая предыдущие формулы, имеем.
\[\oint_{L} E d l=\oint_{A}^{B} E d l=\varphi 1-\varphi 2=\varphi 2-\varphi 1=0\]
Из этого легко сделать вывод, что циркуляция вектора напряжённости по контуру, если он замкнут, равняется нулю. E и dl – векторные величины.
Электродвижущей силой в теории электричества принято считать циркуляцию вектора напряжённости по произвольному замкнутому контуру.
\[\varepsilon=\oint_{L} E d l=0\]
Если поле электростатическое, то ЭДС замкнутого контура (каким бы он ни был) равна нулю.
Закон Ома для участка цепи с электродвижущей силой тока
Рассмотрим один из самых простых случаев – электрическую цепь с химическим источником ЭДС, элементом Вольта. Он состоит из двух электродов (медного и цинкового), погружённых в раствор кислоты.
Электродвижущая сила в этом случае создаётся следующим образом: цинк при растворении в кислоте теряет положительно заряженные атомы, приобретая тем самым отрицательный потенциал, а медь становится положительно заряженной. В результате возникает сторонняя ЭДС. Находится она в очень тонком слое, отделяющем электролит от цинкового и медного электродов. Когда цепь замыкают, на сопротивлениях двух частей цепи (внешней и внутренней) возникает разность потенциалов и начинает течь ток I.
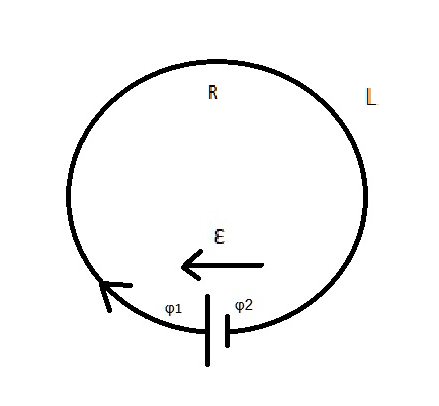
Для простоты расчётов будем исходить из того, что сопротивления на всех участках цепи распределены равномерно по всему контуру L.
Из закона сохранения энергии следует, что работа, совершаемая электрическим полем при движении заряда q по внешней цепи и в электролите будет равняться
Aq = (φ1 – φ2)*q + (φ3 – φ4)*q
Общую работу сторонних сил можно записать как
Ɛq= Ast = (φ3 – φ2)*q + (φ1 – φ4)*q
Приравняв обе части двух предыдущих выражений, получим
Aq= Ast
Формула явно указывает на то, что работа сторонних сил и работа электрического поля равны между собой.
Из закона Ома следует, что
φ1 – φ2 = I*R, а φ3 – φ4 = I*r
От сюда следующий вид закона Ома с электродвижущей силой.
Ɛ = I*(R + r)
Справедлив он только для замкнутой цепи.
О втором правиле Кирхгофа
Полученная формула говорит, что электродвижущая сила равна сложенным друг с другом произведениям силы тока на все сопротивления, составляющих замкнутую цепь.
Ɛ = I*R + I*r
Это очень важное утверждение. Часто его именуют Вторым правилом Кирхгофа. Оно относится ко всем замкнутым цепям, какими бы они ни были.
По-другому это правило можно сформулировать так – в любом электрическом замкнутом контуре алгебраическая сумма произведений сил токов на сопротивления, через которые они протекают равняется ЭДС в указанном контуре.
Сопротивления могут считаться не только положительными, но и отрицательными. Если направление тока совпадает с выбранным направлением обхода контура, то сопротивление признают положительным. Если не совпадает – отрицательным.
Электродвижущая сила тока считается положительной, в том случае, если в его источнике произошёл переход от отрицательного полюса к положительному.
Когда в направлении токов нельзя быть уверенным, его можно выбрать произвольно. Из-за этого после вычислений может получиться отрицательное число. Это признак того что на самом деле ток идёт в противоположную сторону.
Впрочем, здесь всё условно. У многих ток ассоциируется с бегущими по проводнику отрицательно заряженными электронами. Тем не менее за направление тока всегда принимают именно направление положительных движущихся зарядов. Расчётам и пониманию сути физических явлений, относящихся к этому разделу физики подобное никак не мешает. Разве что в самом начале, пока не появилась привычка.
Математическая запись правила Кирхгофа выглядит следующим образом:
\[\sum_{m=1}^{N} \varepsilon m=\sum_{m=1}^{N} I m R m\].
N – число участков, на которые мы разбили контур.
Данная формула позволяет очень легко рассчитывать достаточно сложные цепи, т. к. получаем систему независимых уравнений, легко решаемую с математической точки зрения. То что самостоятельно, на листе бумаги расчёты будут громоздкими – не проблема. Даже простейший не очень мощный компьютер с вычислениями может справиться весьма быстро.
Количество независимых контуров определяется по формуле:
\[n2 = p – m + 1\].
p – общее количество ветвей в цепи, m – общее количество узлов в цепи.














