Изохорный процесс в термодинамике
Изохорный (изохорический) процесс относится к основным процессам термодинамики и возможен исключительно при постоянном объеме. При этом два других параметра, а именно, давление и температура, изменяются.
В термодинамике давление, объем и температуру называют макроскопическим параметрами. В каждом из трех изопроцессов один из макроскопических параметров остается неизменным.
Изопроцессами, в свою очередь, называют изменение термодинамических систем макроскопических тел.
Как уже отмечалось, в изохорном процессе неизменен объем, в изотермическом постоянной остается температура, в изобарическом – давление.
Наиболее удобно рассматривать термодинамические процессы на примере идеальных газов.
Условие осуществления изохорного процесса в идеальном газе
Необходимым и достаточным условием для протекания изопроцесса в идеальном газе или жидкости является постепенное изменение – увеличение или уменьшение – температуры вещества, в котором происходит процесс. Первоначальный объем вещества должен оставаться неизменным, для чего вещество помещается в замкнутое пространство, т. е. в закрытый сосуд.
Зависимость температуры и давления идеального газа в изохорном процессе
В изохорном процессе давление идеального газа всегда прямо пропорционально его температуре. В реальных газах эта зависимость не выполняется.
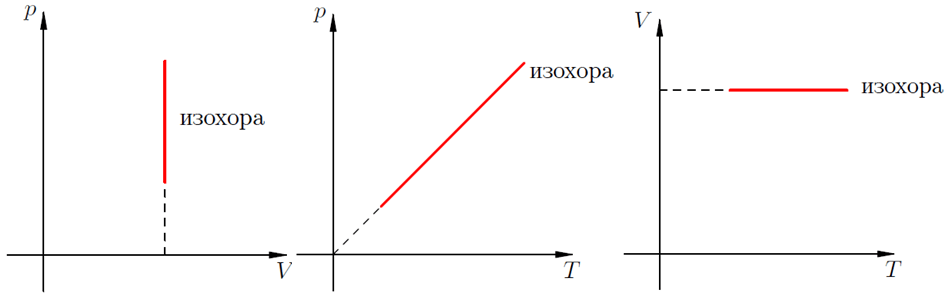
На графиках такое физическое явление как изохорный нагрев (охлаждение) отображает изохора. Это линия, связывающая три физических параметра:
- температуру рабочего тела (вещества) – T;
- объем рабочего тела (вещества) – V;
- внутренне давление – Р.
Для идеальных газов изохоры всегда являются прямыми линиями.
Возникновение и развитие теории изохорного процесса
В 1702 году французский физик-механик, член Французской Академии наук, Гийом Амонтон опубликовал свою работу «Парижские мемуары». В ней ученый подробно описал свои наблюдения за поведением фиксированного объема идеального газа в «стабильном воздушном термометре», в котором жидкость, под влиянием энергии газа в резервуаре и атмосферного давления, находилась в равновесии. При постепенном нагревании давление газа увеличивалось пропорционально температуре, и жидкость вытеснялась, заполняя следующий выступающий столб.
Дальнейшее развитие изучение изохорного процесса газа получило благодаря экспериментам английского физика Джона Дальтона. В своих экспериментах ученый определил, что при совпадающих начальных и конечных показателях, а также при постоянном давлении, все газы и пары при изменении температуры сжимаются или расширяются одинаково. Результаты исследований Джон Дальтон опубликовал в 1801 году.
Через некоторое время полученные Дальтоном результаты смог подтвердить и член Французской Академии наук, физик Жозеф Луи Гей-Люссак. Ученый провел свои независимые опыты и также выявил одинаковое распределение различных газов с практически тем же коэффициентом, что и Дальтон. Свои исследования Гей-Люссак объединил с законом Бойля-Мариотта, благодаря чему впоследствии удалось более подробно описать изохорный процесс. А закон пропорциональной зависимости объема газа от температуры в изохорическом процессе получил название закона Гей-Люсака.
Первый закон термодинамики для изохорного процесса
Формула первого закона термодинамики имеет следующий вид:
\[\boldsymbol{Q=\Delta U+A}\]
Где Q – количество теплоты, \[\boldsymbol{\Delta U}\] – сумма изменения внутренней энергии, A – работа системы.
Закон подразумевает, что для каких-либо изменений внутри системы необходимо приложить внешние усилия. Таким образом, можно предложить следующую простейшую формулировку первого закона термодинамики: для изменения внутренней энергии некоторой системы требуется внешнее воздействие. Именно этот закон доказывает невозможность изобретения вечного двигателя, над которым так долго бились ведущие ученые разных стран.
Изохорный процесс:
- Процесс, происходящий с газом неизменной массы при постоянном объеме называется изохорным.
- Закон Шарля: при изохорном нагревании газа относительное изменение его давления пропорционально конечной температуре.
Как уже отмечалось, изохорным процессом в термодинамике считается физическое явление, протекающее при постоянном объеме. То есть при изменении температуры некоторого газа, находящегося внутри сосуда, его объем не изменится. Следовательно, работа, совершаемая газом при \[V=c o n s t\], равна нулю, т.е. A=0.
Таким образом, первый закон термодинамики для изохорного процесса выражается следующей формулой:
\[\boldsymbol{Q=\Delta U=U\left(T_{2}\right)-U\left(T_{1}\right)}\]
Где \[\boldsymbol{U\left(T_{1}\right)}\] – внутренняя энергия идеального газа при начальной температуре, \[\boldsymbol{U\left(T_{2}\right)}\] – внутренняя энергия идеального газа при конечной температуре.
При изохорном нагреве внутренняя энергия газа возрастает за счет поглощения тепла \[(Q>0)\], а при охлаждении газ отдает тепло и его внутренняя энергия уменьшается \[(Q<0)\].
Изучения термодинамических изменений подразумевает под собой определение следующих параметров: работы, которая была совершена в данном процессе, изменения внутренней энергии и количества теплоты. Также определяется взаимосвязь некоторых величие, характеризующих состояние газа.
Исследование изохорических процессов проводится по следующему методу:
- устанавливается взаимосвязь показателями рабочего тела на начальный и конечный момент, то есть выводится физическое уравнение;
- определяется работа, совершаемая газом, при изменении объема;
- определяется количество подводимой/отводимой теплоты;
- вычисляется изменение внутренней энергии и энтропии (функции состояния исследуемой системы).

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Эффект изохорного процесса и его применение
Свойства изохорного процесса, так же как и свойства изобарного и изотермического процессов, широко применяются в современных изобретениях.
Главный эффект изохорного процесса заключается в том, что при неизменном объеме теплоемкость значительно ниже, чем при постоянном давлении. Теплоемкость – величина, показывающая, какое количество теплоты необходимо для нагрева тела на один градус.
В изохорном процессе при изменении температуры система не совершает никакой работы, и, следовательно, вся подведенная теплота расходуется на изменение тепловой энергии: \[d U=D q\].
Согласно закону Шарля, в идеальном газе при изохорном процессе изменение давления прямо пропорционально изменению температуры. Однако для неидеальных газов закон Шарля не применим. Так как в этом случае некоторая часть теплоты, сообщаемой газу, расходуется на увеличение энергетического потенциала взаимодействия элементарных частиц.
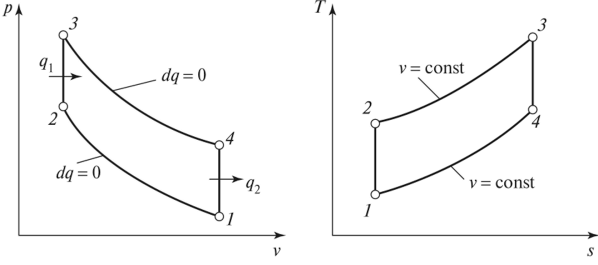
В бензиновом двигателе внутреннего сгорания, в работе которого в максимальном приближении внедрен идеальный цикл Отто, такты 2-3 и 4-1 являются изохорными процессами. 2-3 – изохорный подвод тепла, 4-1 – изохорный отвод тепла. Работа, которая совершается на выходе мотора, равна разности основных работ. То есть разности между работой, совершаемой газом во время рабочего хода (над поршнем во время третьего такта), и работой, затрачиваемой поршнем на сжатие газа во втором такте. Принудительное сжигание смеси, используемое в таких двигателях, позволяет увеличить степень сжатия газа в 7-12 раз.
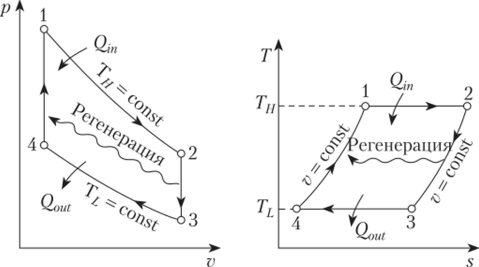
Изохорные такты также присутствуют в двигателях с циклом Стирлинга. В таких двигателях установлен регенератор, обеспечивающий выполнение изохорного процесса в двух тактах. Проходя через наполнитель в одну сторону, газ передает регенератору тепловую энергию рабочего тела. Двигаясь в обратном направлении, газ снова возвращает энергию рабочей системе. КПД и обратимость идеального цикла Стирлинга равны показателям цикла Карно.
Также изохорный подвод тепла используется в циклах ГТУ – газотурбинных установок.














