Система отсчета
Что такое система отсчета
Система отсчета – состоит из абстрактной системы координат и набора физических опорных точек, которые фиксируют систему координат приборами для измерения времени и стандартизируют измерения в этой системе координат.
Система отсчета бывает двух видов:
- Инерциальная система отсчета — это система отсчета, в которой выполняется закон Ньютона. Это означает, что, если на тело не действует никакая внешняя сила, оно останется в покое или будет оставаться в постоянном движении. Предположим, что тело удерживается на поверхности Земли: для человека на Земле оно находится в состоянии покоя, а для человека на Луне оно находится в движении. Таким образом, более общее определение инерциальной системы отсчета будет следующим: инерциальная система отсчета находится в состоянии покоя или движется с постоянной скоростью по отношению к предполагаемой инерциальной системе отсчета.
- Неинерциальная система отсчета. Вы можете определить неинерциальную систему отсчета как ускоренную систему отсчета относительно принятой инерциальной системы отсчета. В этом контексте закон Ньютона не будет соблюдаться. Итак, из приведенного выше примера: если Земля считается инерциальной системой отсчета, Луна становится неинерциальной системой отсчета, потому что она находится в ускоренном движении относительно Земли.
Аффинная и декартова системы координат
Если рассматривать все системы отсчета с кинематической точки зрения, они похожи. Кинематика не указывает на преимущества одной системы отсчета перед другой. Для удобства решения была выбрана наиболее приемлемая система. Чтобы описать пространство, в котором движется материальная точка, система отсчета связана с системой пространственных координат.
Система пространственных координат — это набор определений, которые могут реализовать метод координат, то есть определение положения точки или тела с помощью чисел или символов.
Числа, которые могут обозначать положение выбранной точки в трехмерном пространстве, называются координатами этой точки.
Аффинная система координат
Аффинная система координат образована тремя линейно независимыми векторами (осями координат), исходящими из точки, то есть из начала координат.
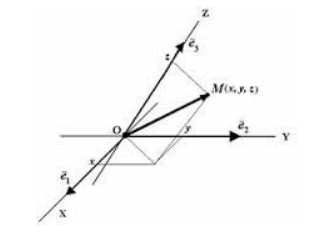
Этот случай показывает, что положение материальной точки MM в пространстве определяется радиус-вектором проведенным через начало системы координат в данную точку, движение можно представить как сумму векторов независимых перемещений вдоль три пространственные оси выбранной системы координат
Декартова система координат
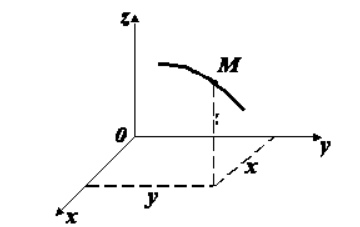
Декартовы координаты позволяют определять положение точки на плоскости или трехмерном пространстве. Декартовы координаты (также называемые прямоугольными координатами) точки — это пара чисел (в двух измерениях) или тройка чисел (в трех измерениях), которые определяют расстояния со знаком от оси координат.
Чаще всего используется декартова система координат, состоящая из взаимно перпендикулярных осей x, y, z Данная система применима для описания прямолинейного движения и движения по разомкнутым или нециклическим кривым. Это визуальная геометрическая интерпретация с простыми вычислениями.
Цилиндрическая и сферическая системы координат
Декартова система координат обеспечивает простой способ описания расположения точек в пространстве. Однако некоторые поверхности сложно смоделировать с помощью уравнений, основанных на декартовой системе. Рассмотрим два разных способа описания положения точек в пространстве, оба из которых основаны на расширениях полярных координат. Как следует из названия, цилиндрические координаты полезны для решения задач, связанных с цилиндрами, таких как расчет объема круглого резервуара для воды или количества масла, протекающего по трубе. Точно так же сферические координаты полезны для решения задач, связанных со сферами.
Цилиндрическая система координат
Когда мы расширили традиционную декартову систему координат с двух измерений до трех, мы просто добавили новую ось для моделирования третьего измерения. Начиная с полярных координат, мы можем следовать тому же процессу, чтобы создать новую трехмерную систему координат, называемую цилиндрической системой координат. Таким образом, цилиндрические координаты обеспечивают естественное расширение полярных координат до трех измерений.
В цилиндрической системе координат точка в пространстве (рис. 3) представлена упорядоченными тремя скалярами \[(\tau, \theta, z)\] где \[(\tau, \theta)\] полярные координаты проекции точки на плоскость \[x y\], а z-координата в декартовой системе координат.
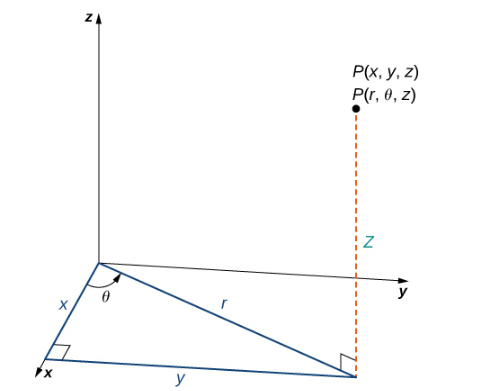
Длина гипотенузы равна r и θ — мера угла, образованного положительной осью x и гипотенузой. Г координата описывает местоположение точки выше или ниже х плоскости.
На плоскости xy прямоугольный треугольник, показанный на рис. 3, дает ключ к преобразованию между цилиндрическими и декартовыми (прямоугольными) координатами.
Преобразование между цилиндрическими и декартовыми координатами
Прямоугольные координаты (x,y,z) и цилиндрические координаты (r,θ,z) точки связаны следующим образом:
\[\boldsymbol{z}=\boldsymbol{z}\] и \[r^{2}=x^{2}+y^{2}\]
\[\boldsymbol{z}=\boldsymbol{z}\]

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Сферическая система координат
В декартовой системе координат положение точки в пространстве описывается с помощью упорядоченной тройки осей, в которой каждая координата представляет собой расстояние. В цилиндрической системе координат положение точки в пространстве описывается двумя расстояниями (r и z ) и угла (θ). В сферической системе координат мы снова используем упорядоченную тройку осей для описания положения точки в пространстве. В данном случае оси описывают одно расстояние и два угла. Сферические координаты упрощают описание сферы, так же как цилиндрические координаты упрощают описание цилиндра. Линии сетки для сферических координат основаны на измерениях углов, как и для полярных координат.
В сферической системе координат точка P в пространстве (рис. 4) представлена упорядоченной тройкой
\[(\rho, \theta, \varphi)\]
Где:
\[\rho\] — это расстояние между P и началом координат \[(p \neq 0)\];
\[\boldsymbol{\theta}\] — тот же угол, который используется для описания местоположения в цилиндрических
координатах;
\[\varphi\] — это угол, образованный положительной осью z и отрезком прямой OP, где О это начало
координат и \[0 \leq \varphi \leq \pi\]
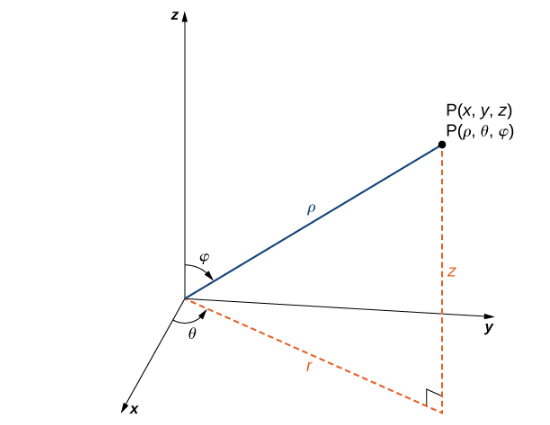
Условно начало координат представлено как (0,0,0) в сферических координатах.
Преобразование между сферическими, цилиндрическими и прямоугольными координатами
Декартовые координаты \[(x, y, z)\] и сферические координаты \[(\rho, \theta, \varphi)\] связаны следующим образом:
\[y=\rho \sin \varphi \sin \theta\] — уравнения для преобразования из сферических координат в квадратные (декартовы).
\[z=\rho \cos \varphi\] и \[\rho^{2}=x^{2}+y^{2}+z^{2}\]
\[\tan \theta=\frac{y}{x}\] — уравнения для преобразования из декартовых в сферические.
Если точка имеет цилиндрические координаты \[(r, \theta, z)\], тогда эти уравнения определяют связь между цилиндрическими и сферическими координатами.
\[r=\rho \sin \varphi\]
\[\boldsymbol{\theta}=\boldsymbol{\theta}\] — уравнения для преобразования из сферических координат в цилиндрические.
\[z=\rho \cos \varphi\] и \[\rho=\sqrt{r^{2}+z^{2}}\]
\[\boldsymbol{\theta}=\boldsymbol{\theta}\] — уравнения для преобразования из цилиндрических в сферические.
Формулы для преобразования сферических координат в прямоугольные могут показаться сложными, но это простые приложения тригонометрии. Глядя на рисунок 5, легко увидеть, что \[r=\rho \sin \varphi\]. Затем, глядя на треугольник на плоскости xy с \[\boldsymbol{\rho}\] в качестве его гипотенузы имеем \[x=r \cos \theta=\rho \sin \varphi \cos \theta\]. Вывод формулы для y похож. Рисунок 3 также показывает, что \[p^{2}=r^{2}+z^{\alpha}=x^{2}+y^{2}+z^{2}\] и \[z=\rho \cos \varphi\]. Решая это последнее уравнение для \[\varphi\] а затем подставив \[p=\sqrt{\boldsymbol{r}^{2}+\boldsymbol{z}^{2}}\] (из первого уравнения) дает \[\varphi=\arccos \left(\frac{z}{\sqrt{r^{\alpha}+z^{2}}}\right)\]. Также обратите внимание, что, как и прежде, мы должны быть осторожны при использовании формулы \[\tan \theta=\frac{y}{z}\] выбрать правильное значение \[\theta\].
Существуют и другие криволинейные системы координат, с помощью которых можно найти координаты заданной точки: параболические, гиперболические, эллиптические и другие. Система отсчета подбирается для каждого случая индивидуально с учетом особенности движения тела, с помощью которой определяется простейший закон движения того или иного тела или точки.














