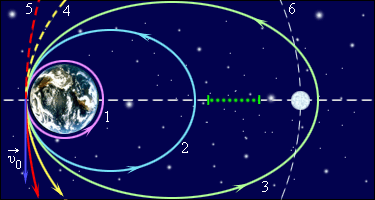
Космические скорости
Первая космическая скорость
Для того чтобы движение вокруг Земли осуществлялось по круговой орбите, тело, которое осуществляет движение, должно обладать некой определенной скоростью. Которая определяется из условия равенства. А именно: произведение массы тела на показатель ускорения силы тяжести, которая действует на тело.
Движение проходит по круговой орбите с заданным радиусом, который схож с радиусом земли R.
Первая космическая скорость \[\boldsymbol{(\left.\vartheta_{1}\right)}\] — это показатель необходимый для того, чтобы тело имело возможность стать спутником Земли.
Формула первой космической скорости будет иметь следующий вид:
\[\vartheta_{1}=\sqrt{g R_{3}}=8 \mathrm{км} / \mathrm{с}.\]
Вторая космическая скорость
В случае, когда тело обладает первой космической скоростью \[\vartheta_{1}\], будет наблюдаться поступательное, стабильное движение, которое не падает на протяжении всего своего пути следования. Однако данной скорости недостаточно для выхода из сферы земного притяжения. Иными словами, иметь возможность удалиться от Земли на определенное расстояние. При этом также наблюдается потеря силы телом.
Чтобы выполнить все данные действия, необходима вторая космическая скорость. Также можно встретить термин, скорости убегания.
Чтобы определить значение второй космической скорости, необходимо выполнить следующее действие: вычислить показатель работы, которая потрачена против сил земного притяжения при соударении с поверхность. Земли.
При ударении данного тела получаем следующую формулу:
Где:
- m — масса брошенного тела;
- М — масса планеты;
- r — значение радиуса планеты;
- h — расстояние от основания до центра масс;
- G — постоянная гравитационной силы;
- \[\boldsymbol{\vartheta_{2}}\] — показатель второй космической скорости.
Решим уравнение относительно значения \[\boldsymbol{\vartheta_{2}}\], и получим следующую формулу:
Между двумя космическими скоростями существует взаимосвязь, которую можно выразить в виде формулы:
Определение квадрата скорости убегания можно определить по формуле:
Вторая космическая скорость, исходя из сравнений, больше чем первая в \[\sqrt{2}\] раза. Если перемножить 8 км/с на \[\sqrt{2}\] , то получим значение равное 11 км/с. Следовательно вторая скорость будет выше , чем первая.
Необходимая величина скорости не зависит от направления движения рассматриваемого тела.
На скорость будет влиять следующий показатель: траектория, по которой осуществляется удаление от поверхности земли. Чтобы тело смогло начать движение с поверхности планеты, ему необходимо обладать второй космической скоростью. При наименьшем значении h и большом показателе гравитационной силы. Как только ракета начнет заметно удаляться от Земли, гравитационная постоянная сила будет уменьшаться. Также будет уменьшаться и значение, необходимое для удаления кинетической энергии.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Третья космическая скорость
Когда тело выходит за пределы солнечной системы, ему необходимо преодолеть силу притяжения к Земле и к Солнцу. Для этого необходима третья космическая скорость \[\vartheta_{3}\] . Данная скорость позволяет осуществлять запуск тела с поверхности земли.
Значение данного показателя будет зависеть от направления движения. Когда запуск будет производится в направлении относительно орбитального движения Земли, то значение скорости будет минимальным, и составит около 17 км/. При запуске тела в противоположном направлении движения Земли, скоростное значение будет равно приблизительно 73 км/ч.
Пример решения задачи с применением основных формул
Необходимо определить космическую скорость для спутника планеты Юпитер, который летает на минимальной высоте,
при массе планеты равной \[1,9 \cdot 10^{27}\]кг, Радиус равен \[R=7,13 \cdot 10^{7}\]м.
Заданы следующие значения:
- \[\mathrm{B}=1.9 \cdot 10^{27}кг;\]
- \[\mathrm{R}=7,13 \cdot 10^{7}м.\]
Необходимо вычислить значение первой космической скорости.
Запишем формулу для нахождения первой космической скорости: \[\vartheta_{1}=\sqrt{g R_{3}}\].
Значение g принимает показатель ускорения свободного падения на планете Юпитер.
Применяя закон всемирного тяготения получаем следующее выражение: \[m g=G \frac{m M}{r^{2}}\].
Показатель m принимается как масса спутника планеты. Значение M — это масса самой планеты.
Если высота спутника над поверхностью Юпитера небольшая относительно его значения радиуса, тогда данной высотой разрешается пренебречь: \[r=R\].
Используя второе уравнение, можем определить ускорение свободного падения планеты: \[g=G \frac{M}{R}\].
Далее подставим в уравнение все известные значения и определим необходимы показатель:
\[\vartheta_{1}=\sqrt{g R_{3}}=42159,45 \mathrm{м} / \mathrm{с}\]
Ответ: \[\vartheta_{1}=\sqrt{g R_{3}}=42159,45 \mathrm{м} / \mathrm{с}\].
Интересные факты
Космические показатели были достигнуты еще в СССР. Первый запуск искусственного спутника был осуществлен в 1957 году.
В 1959 ученые смогли найти решение для преодоления сферы земного притяжения.
В 1961 году был осуществлен первый полет в космическое пространство человеком. Первым космонавтом стал Юрий Алексеевич Гагарин. Который совершил удачный полет вокруг земли.
Космические скорости можно рассчитать для различного удаления от центра Земли. В астрономии и космонавтике чаще всего используются показатели и величины, которые рассчитаны для однородной модели Земли. При расчете используется величина радиуса равная 6371 км. В данном случае каждая скорость обладает одним конкретным значением.
Первая космическая скорость равна 7,910 км/с, вторая – 11,186 км/с, третья – 16,67 км/с.