Теорема Гаусса
До того, как мы рассмотрим теорему Гаусса, поговорим о том, кто же ее открыл и применил на практике.
Карл Фридрих Гаусс 1777-1855 г. Немецкий математик — один из великих, который не уступает Ньютону и Архимеду. Родился в Брауншвейге, в крестьянской семье.
Гениальная способность к математике проявилась уже в детстве и, пораженный чудесным талантом, учитель начальных классов убеждал родителей Карла не отдавать мальчика в ремесленную школу, а предоставить возможность продолжить образование. В четырнадцать лет Гаусс буквально удивился своим обширным знанием графа Брауншвейгского, и он дал юноше стипендию.
Большую часть своих важных математических исследований Гаусс сделал до того, как в 1799 г. он получил ученую степень доктора наук в Гёттингенском университете, а через два года выпустил свой фундаментальный труд «Трактат о математике», посвященный его влиятельному покровителю.

В трактате речь шла об арифметике — разделе математики, который занимается, прежде всего, натуральными числами и отношениями между ним, например, такими как Великая теорема Ферма. Впоследствии Гаусс не оставил свои занятия математикой, формулируя ряд принципов теоретической вероятности и математики, в том числе распределения случайной величины вокруг средней величины, которое было названо распределением Гаусса.
В 1801 г., когда был открыт первый астероид Церера, Гаусс обратился к астрологии. Чтобы рассчитать параметры орбиты, он разработал методику наименьшего квадрата, которая позволяет полностью рассчитывать орбиту солнечного спутника по результатам только трех измерений положения его места на орбите около Солнца. Через пять лет ученый был назначен директором Гёттингенской обсерватория и остался на этом посту до конца своей жизни. К тому же Гаусс был первым, кто всерьёз занимался изучением земной магнетизма, и именно в честь него названа единица магнитной напряженности.
В науке нередко бывает так, что один и тот же закон может быть сформулирован по-разному. В большинстве случаев формулировка закона не меняет ничего в плане его действий, но новые формулировки помогают теоретикам чуть иначе трактовать его и проверять его в отношении новых природных явлений. Именно таким образом можно рассмотреть теорему Гаусса — это, по сути, обобщение закона Кулона, который, в своей очередь, был обобщением всех знаний ученых об электростатических зарядах.
В математике, физике, астрономии найдется немного областей, развитию которых не посодействовал замечательный гений Карла Фридриха Гаусса.
В 1831 г. вместе с юным коллегой Вильгельмом Вебером (1804-1891 г.) он начал изучать электричество и магнетизм, вскоре сформулировав и доказав теорему, которая носит его имя. Для понимания её смысла представьте изолированный точечный электрический заряд Q. А сейчас представьте себе, что его окружает замкнутая поверхность. В теореме форма поверхности не важна – это может оказаться даже сдутым воздушным шариком.
В каждой точке окружающей заряд поверхности, наблюдается электрическое поле, образованное зарядом, а произведение напряженности этого электрического поля на сколь угодно малую единицу площади окружающей заряд поверхности, через которую проходят силовые линии поля, называется потоком напряженности электрического поля, и можно рассчитать поток напряженности, приходящийся на каждый элемент поверхности. В теореме Гаусса говорится, что общий поток электрической напряженности, проходящий по окружающей поверхности заряда, пропорционален величине зарядов.
Связь между законом Кулона и теоремой Гаусса можно рассмотреть на простом примере. Предположим, что заряд q окружен сферой радиуса r. На удалении r от заряда напряженность электрического поля, которая определяется силой притяжения или отталкивания единичного заряда, помещенного в соответствующую точку, составит, согласно закону Кулона:
\[E=k q / r^{2}\]
И то же самое значение мы получим для любой точки сферы заданного радиуса. Следовательно, суммарный поток напряженности электрического поля будет равен значению напряженности поля на удалении r от заряда, помноженному на площадь сферы (которая, как известно, равняется 4πr2). Иными словами, суммарный поток будет равен:
Формула теоремы Гаусса
\[4 \pi r^{2} \times k q / r^{2}=4 \pi k q\]
Применение формулы Гаусса
Формула применяется для преобразования объемного интеграла в интеграл на замкнутую поверхность и обратно. В математическом анализе формула Теоремы Остроградского — Гаусса применяется для расчета дифференциации, т.е. потока вектора по поверхности окружающей среды внешними направлениями.
Принимая во внимание то, что поток векторного поля через замкнутую поверхность δδ в направлении внешней единичной нормали n0¯¯¯¯¯n0¯ равен дивергенции данного поля, вычисленной по телу TT, которое эта поверхность.
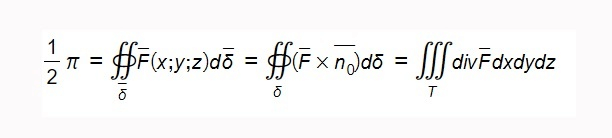

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Применение теоремы Гаусса для электростатического поля
Теорема Остроградского-Гаусса применяется для расчета электростатического поля для тех задач, где поле имеет специальную симметрию. Например, плоскую, цилиндрическую или сферическую. В данном случае на эффективность применения теоремы влияют симметрия и конфигурация поля, которые должны соответствовать двум условиям:
- заряженное тело должно быть окружено простой замкнутой поверхностью;
- вычисление потока вектора напряженности необходимо свести к умножению ЕЕ (или EnEn) на площадь поверхности SS или часть нее.
Если исходные данные не соответствуют условиям, то при решении задачи необходимо использовать другие методы.
Рассмотрим применение теоремы для равномерно заряженной плоскости.
Задача
Предположим, что заряд положительный, а плоскость заряжена с постоянной поверхностной плотностью, что выражается в формуле δ=dqdSδ=dqdS. Благодаря симметрии можно сделать вывод, что напряженность в любой точке поля обладает направлением, перпендикулярным плоскости. Из этого же можно сделать вывод, что во всех точках, симметричных плоскости, напряженность поля одинакова, но ее направление противоположно.
Отметим на заряженной плоскости площадь △S△S. Определим вокруг площадки замкнутую цилиндрическую поверхность (рисунок 3) так, чтобы ее образующие основания были перпендикулярны плоскости, располагались симметрично, относительно нее и имели величину △S△S.
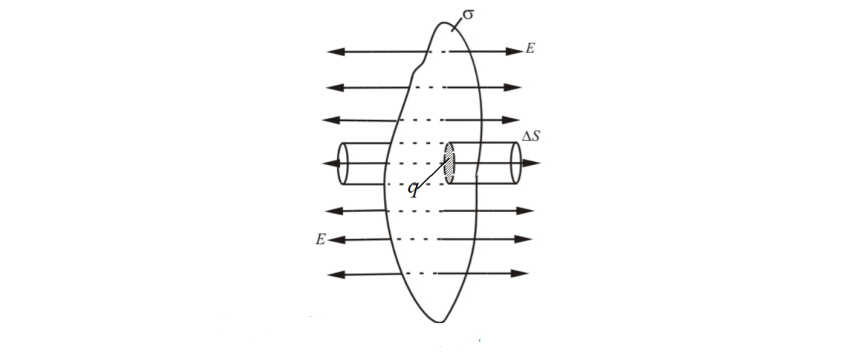
А теперь используем теорему Остроградского-Гаусса: ∮SEndS=1ε0∑q1∮SEndS=1ε0∑q1. Так как в этом случае En=0En=0 в каждой точке, через боковую часть потока не будет. В случае оснований En=EEn=E, а исходя из этого совокупный поток через поверхность равен 2E△S2E△S.
Посмотрим теперь внутрь поверхности. Там заключен заряд δ△Sδ△S. В соответствии с теоремой Остроградского-Гаусса, должно быть выполнено условие: 2E△S=δ△Sε02E△S=δ△Sε0, из чего следует E=δ2ε0E=δ2ε0.
Так как напряженность поля равна на любых расстояниях от плоскости, в вычисления не нужно включать длину цилиндра. Если плоскость заряжена, то направление векторов изменяется на противоположное.
Поток вектора напряженности в теореме Гаусса
Поток вектора напряженности электрического поля через замкнутую поверхность в вакууме равен алгебраической сумме всех зарядов, расположенных внутри поверхности, деленной на ε0 (поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность S.)

С помощью дифференциальной формы теоремы можно рассчитать электростатическое поле при произвольном пространственном распределении зарядов. В ней установлена связь между объемной плотностью заряда ρ и изменением Е в окрестности данной точки пространства.














