Уравнение Майера
Уравнение Майера математически показывает связь между теплоемкостями идеального газа при течении двух изопроцессов. Данное выражение устанавливает соотношение между единицами измерения количества теплоты и единицами механической работы.
Теплоемкость в уравнении Майера
Теплоемкостью тела называется количество теплоты, которое было сообщено телу для повышения его температуры на 1 градус Кельвина. Эта величина обозначается буквой «C». Математически представленное определение можно записать в виде:
\[C=\frac{\delta Q}{d T}\]
Количество теплоты, которое требуется для нагревания на 1 К одного моля вещества, называется молярной теплоемкостью. В таком случае соотношение будет выглядеть так:
\[C_{\mu}=\frac{C}{v}\]
Здесь υ – это количество вещества (в моль). Теплоемкость в уравнении Майера является одной из составляющих.
Параметр теплоемкости не является функцией, описывающей состояние системы. Она характеризует бесконечно близкое состояние системы Теплоемкость может выражаться как функция, описывающая бесконечно малый процесс, который совершается в системе.
Математическое соотношение для теплоемкости может быть записано в дифференциальном виде. Применяя первое начало термодинамики, получим:
\[C=\frac{\delta Q}{d T}=\frac{d U+p d V}{d T}\]
Уравнение Майера для идеального газа
Термодинамическая система характеризуется тремя основными параметрами:
- давлением (p),
- температурой (T),
- объемом (V).
Связь между ними показывает соотношение Менделеева-Клапейрона. Эта формула носит название уравнения состояния. Зависимость одного параметра от другого можно записать относительно каждой составляющей:
p = p(T, V) или T = T( p , V ) , V = V( p , T ).
Внутренняя энергия (U) термодинамической системы является функцией от двух независимых переменных, в качестве которых выбираются объем и температура, то есть: U = U(T, V). Отсюда можно получить соотношение для полного дифференциала от внутренней энергии:
\[d U=\left(\frac{\partial U}{\partial T}\right)_{V} d T+\left(\frac{\partial U}{\partial V}\right)_{T} d V\]
Подставив это выражение в дифференциальное уравнение теплоемкости, получим следующее:
\[\left.C=\frac{\left(\frac{\partial U}{\partial T}\right)_{V} d T+\left(\frac{\partial U}{\partial V}\right)_{T} d V+p d V}{d T}=\left(\frac{\partial U}{\partial T}\right)_{V}+o p e n p+\left(\frac{\partial U}{\partial V}\right)_{T}\right] \frac{d V}{d T}\]
Полученная формула показывает, что параметр теплоемкости зависит от процесса, в котором участвует тело. В случае с изохорным процессом (dV/dT)=0. При течении процесса, в котором объем тела остается постоянным, теплоемкость может быть определена как:
\[C_{V}=\left(\frac{d U}{d T}\right)_{V}\]
Для изобарного процесса (давление постоянно) тот же параметр будет определяться как:
С учетом полученных выражений, можно сделать вывод, что количество теплоты, переданного телу, будет определяться самим процессом, в котором данное тело участвует.
На рисунке ниже схематично представлены два процесса – изохорный и изобарный. В обоих случаях происходит нагревание газа (T2 > T1).
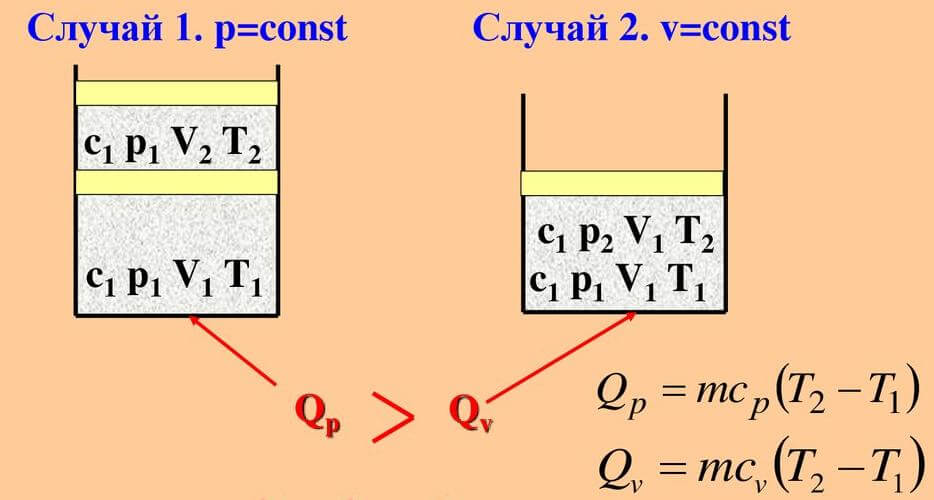
Вывод уравнения Майера
В термодинамике вывод уравнения Майера осуществляется на основе уравнения состояния идеального газа.
Сделаем математическую запись малого приращения энергии идеального газа:
\[d U=\frac{i}{2} v R d T\]
Здесь R – универсальная газовая постоянная, а i – число степеней свободы.
Из этого выражения следует, что \[\left(\frac{\partial U}{\partial V}\right)_{T}=0\]. Запишем уравнение Менделеева-Клапейрона, с помощью которого описывается состояние идеального газа:
\[p V=v R T\]
Исходя из этого, можем записать следующее соотношение:
\[\left(\frac{\partial V}{\partial T}\right)_{p}=\frac{uR}{p}\]
Теперь подставим два последних выражения в уравнение теплоемкости при постоянном давлении:
\[\left.C_{p}=C_{V}+\text { openp }+0\right] \frac{v R}{p}=C_{V}+v R\]
Полученная формула есть уравнение Майера для идеального газа. Для случаев нагревания молярного количества вещества это выражение примет вид:
\[C_{\mu p}=C_{\mu V}+R\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Применение уравнения Майера в термодинамике
Оба вида уравнения Майера в термодинамике нашли своё практическое применение при решении задач. Ниже в виде таблицы представлены данные задачи:
| Параметры | Значения |
| Масса кислорода, \[m_{O_{2}}\] | 32 г |
| Масса гелия, \[m_{H e}\] | 20 г |
| Процесс | Изобарный |
| Удельная теплоемкость смеси | ? |
Количество теплоты, которое получила газовая смесь, будет рассчитываться по формуле:
\[Q=C_{p} m \Delta T\]
Здесь m – это масса смеси, ΔТ – разность температур, а cp – искомый параметр. Это количество теплоты складывается из тепла, полученного каждым веществом по-отдельности. Для кислорода:
\[Q_{O_{2}}= c_{pO_{2}}m_{O_{2}}\triangle T\]
Аналогично для гелия:
\[Q_{Не}= c_{рНе}m_{Не}\triangle T\]
В итоге получаем выражение:
\[Q=c_{p}m\triangle T = Q_{O_{2}} + Q_{He} = c_{pO_{2}}m_{O_{2}}\triangle T + c_{pHe}m_{pHe}\triangle T\]
Руководствуясь законом сохранения массы, делаем вывод, что общая масса смеси будет равна: \[m = m_{O_{2}}+m_{He}\].
Из формулы для общего количества теплоты выразим искомую величину:
\[c_{p}=\frac{C_{p O_{2}} m_{O_{2}}+C_{p H e} m_{H e}}{m_{O_{2}}+m_{H e}}\]
Запишем формулу удельной теплоемкости через молярную, используя закономерную связь между этими параметрами:
Приведем формулу уравнения Майера:
Для гелия \[i_{H e}=3\], для кислорода \[i_{O_{2}}=5\]. С учетом этого запишем:
В результате можем записать окончательное выражение для нахождения требуемой величины:
\[c_{p}=\frac{\frac{\frac{7}{2} R}{\mu_{O_{2}}} m_{O_{2}}+\frac{\frac{5}{2} R}{\mu_{H e}} m_{H e}}{m_{O_{2}}+m_{H e}}\]
Теперь подставим имеющиеся значения и найдем ответ:
\[c_{p}=\frac{\frac{\frac{7}{2} * 8,31 * 32}{32}+\frac{\frac{5}{2} * 8,31 * 20}{4}}{32+20}=2,55\left(\frac{Д ж}{K}\right)\]
Еще один практический пример применения уравнения – определение соотношений между единицами измерения энергий. Английский ученый Джоуль установил, что разность \[\left(c_{\mu p}-c_{\mu V}\right)\] численно равняется 1,986 (кал/К*моль). Значение универсальной газовой постоянной в других единицах измерения работы составляет \[R=8,314 * 10^{7}\] (эрг/К*моль). Используя полученные значения, необходимо определить соотношение между приведенными единицами измерения.
Из уравнения Майера:
\[c_{\mu p}=c_{\mu V}+R\]
выразим R:
\[R=c_{\mu p}-c_{\mu V}\]
Отсюда следует, что 1,986 (кал/К*моль) = \[8,314 * 10^{7}\] (эрг/К*моль). Поделим оба значения на \[1,986(К * \text { моль })^{-1}\] и получим: 1 кал = \[4,186 * 10^{7}\] эрг. Оба эти значения равняются 4,186 Дж.
Из решения задачи делаем вывод, что 1 эрг = \[1 * 10^{-7}\] Дж; 1 кал = 4,186 Дж.
Физический смысл уравнения Майера
Физический смысл уравнения Майера заключается в следующем. Это соотношение показывает, что удельная теплоемкость в процессе с постоянным давлением всегда больше, чем в процессе с постоянным объемом. При этом разность между ними равняется величине универсальной газовой постоянной. Такое утверждение объясняется тем, что в изобарном процессе газу необходимо большее количество теплоты для того, чтобы совершать работу расширения, поскольку только при увеличении объема газа можно сохранять давление неизменным.
Отношение теплоемкостей изобарного и изохорного процессов называется показателем адиабаты:
\[\gamma=\frac{C_{p}}{C_{V}} *15\]
Оно показывает, во сколько раз теплоемкость тела в изобарном процессе больше, чем в изохорном. Показатель имеет второе название – коэффициент Пуассона. Ниже приведена таблица, в которой указаны значения коэффициента для некоторых типов газов.
| Газ | γ |
| Одноатомный | 1,67 |
| Двухатомный | 1,40 |
| Трехатомный | 1,28 |
Выполнение любых работ по физике
Популярные статьи
Жесткость пружины
Емкость конденсаторов
Диэлектрики: понятие, формулы, примеры
50 основных формул по физике