Вектор индукции магнитного поля
Свойством поля магнитного в любой его точке с позиции силы выступает вектор магнитной индукции \[\overrightarrow{\mathrm{B}}\].
Вектор индукции магнитного поля: главные понятия
Рассмотрим определение вектора индукции магнитного поля. Индукцию определяют как предел отношения F силы, воздействующий на магнитное поле, на ток \[\text { Idl }\] к произведению элементарного тока \[\text { I }\] со значением элемента проводника \[\text { dl }\]. Другими словами, магнитная индукция действует по направлению перпендикулярно \[\perp\] по направлению тока (или по-другому к элементу проводника \[\text { dl }\Rightarrow\] из (1), а также вектор магнитной индукции поля перпендикулярен \[\perp\] к направлению силы, которая действует с магнитного поля.
Вектор магнитной индукции однородного поля и неоднородного
Если \[\overrightarrow{\mathrm{B}}=\mathrm{const}\], то поле является однородным. Если оно не изменяется с течением времени, то про него говорят, что поле постоянное.
Вектор индукции магнитного поля: важные формулы
Важно!
Формула с векторами преобразуется в модульную форму, потому что векторы задают направление, а модульная форма — значения, которые необходимы для решения задачи.
Модуль вектора индукции однородного поля находят следующим образом:
\[\mathrm{B}=\frac{\mathrm{M}_{\max }}{\mathrm{P}_{\mathrm{m}}}\].
где \[\mathrm{M}_{\max }\] — вращающий момент в максимуме действует на контур с элементарным током, помещенный в магнитное поле, где в данном случае \[\mathrm{P}_{\mathrm{m}}=\mathrm{I} \cdot \mathrm{S}\] — магнитный момент контура (S — площадь определенного контура).
Модуль вектора индукции магнитного поля: производные формулы
Есть еще формулы для определения модуля магнитной индукции. Она определяется как отношение силы в максимуме \[\mathrm{F}_{\max }\], которое реагирует на проводник длины (при этом L= 1 м) к силе элементарного тока \[\text { I }\] в проводнике:
В вакууме модуль индукции будет равен:
Чтобы найти вектор индукции через силу Лоренца, следует преобразовать формулу: \[\overrightarrow{\mathrm{F}}=\mathrm{q} \cdot[\overrightarrow{\mathrm{V}} \times \overrightarrow{\mathrm{B}}]\] (Крестом обозначается произведение векторов)
В данном случае угол α — это угол между вектором индукции и скорости. Стоит отметить, что направление силы Лоренца \[\overrightarrow{\mathrm{F}}\] перпендикулярно \[\perp\] каждому вектору, направлено по правилу Буравчика. Под символом q подразумевается заряд в магнитном поле.
В СИ единицей модуля магнитной индукции принимается 1 Тесла (кратко — Тл), где \[1 Tл=\frac{H}{Aм}\]
Как определяется направление вектора индукции магнитного поля?
За направление вектора индукции магнитного поля \[\overrightarrow{\mathrm{B}}\] используют направление, в котором устанавливается под воздействием поля утвердительного нормали к току с контору. Другими словами объясняют так: вектор идет в направление поступательного перемещения правого винта при вращении по направлению передвижения тока внутри контура.
Вектор индукции \[\overrightarrow{\mathrm{B}}\] обладает направлением, которое начинается со стрелки южного полюса \[\text { S }\] (она свободна передвигается в поле) к полюсу северному \[\text { N }\].
Магнитное поле возникает из-за электрических зарядов (элементарными токами), движущиеся в нем.
Для того чтобы определить направление вектора магнитной индукции в проводнике с элементарным током, используют правило правой руки (Буравчика). Они формулируются так:
- Для катушки с током: 4 согнутых пальца руки, которые обхватывают катушку, направляют по течению току. В это время оставленный большой палец на \[90^{\circ}\] указывает на направление магнитной индукции \[\overrightarrow{\mathrm{B}}\] в середине катушки.
- Для прямого проводника с элементарным током: большой палец руки, который оставляется на \[90^{\circ}\], направить по течению элементарного тока. В это время 4 согнутых пальца, которые держат проводник, показывают сторону, куда направлена индукция магнитного поля.
Задания по теме
Разберем примеры, в которых будет задействована данная формула и свойства.
Пример 1
Условие задачи:
Проводник представлен в квадратной форме. Каждая из сторон равна d. В данный момент по нему проходит элементарный ток силы I. Найдите индукцию магнитного поля в месте, где диагонали квадрата пересекаются.
Решение задачи следующее:
Сделаем рисунок, в котором плоскость совпадает с плоскостью проводника. Изобразим направление вектора индукции магнитного поля.
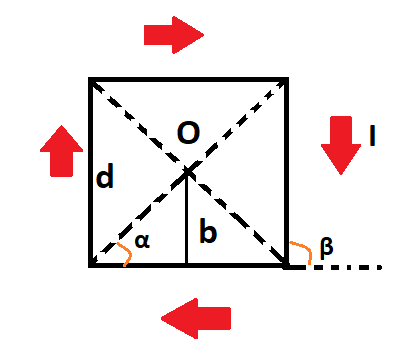
В данной точке О получаются проводники с элементарным током, которые расположены прямолинейно и вектор магнитной индукции поля перпендикулярен плоскости. Направления напряжености полей определяется в соответствием с правилом правого винта,то есть перпендикулярны плоскости изображения. Поэтому сумму векторов по принципу суперпозиции надо заменить на алгебраический вид. Получим следующее выражение: B=B1+B2+B3+B4
Из симметричности рисунка можно увидеть, что модули вектора индукции магнитного поля одинаковы. Получаем следующее: B=4B1
В разделе физике «Электромагнетизм» использовали одну из формул, чтобы рассчитать модуль индукции прямолинейного проводника с элементарным током.
Чтобы формула подошла к данной задачи, ее применяют в следующем виде:
углы α и β, которые отмечены на рисунке:
Используем формулу \[B_{1}=\frac{I \cdot \mu_{0}}{4 \pi b}(\cos \alpha-\cos \beta)\] и преобразуем с применением тригонометрического свойства:
Поскольку у нас квадратная форма, то следует заметить следующее:
Возьмем выведенные формулы и получим конечное выражение, то есть:
Ответ: \[\mathrm{B}=\frac{2 \sqrt{2}}{\pi \mathrm{d}} \cdot \mathrm{I} \cdot \mu_{0}\]

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Пример 2
Условие задачи:
Бесконечно проводник с элементарным током (I) согнут под 90 градусов, который изображен на рисунке. Найдите вектор магнитной индукции однородного поля в точке А.
Решение задачи:
В точке А получается из двух частей проводника, то есть:
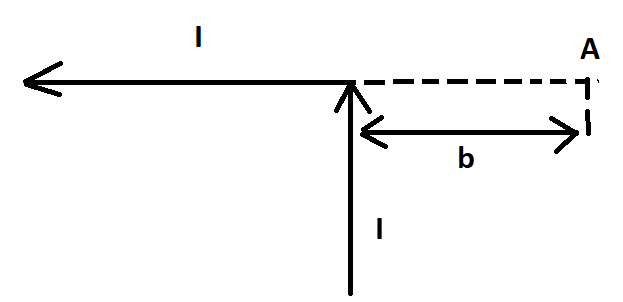
Теперь посмотрим горизонтальный участок, где расположена точка А. Данная область проводника с элементарным током формирует поле в этой точке. Вектор индукции магнитного поля \[\mathrm{B}_{\mathrm{II}}\] равен нулю, потому что в А все углы между с радиус-векторами и с элементарным током равны π.
Следовательно, произведение векторов \[[\mathrm{d} \vec{ l } \vec{r}]\] и поток вектора индукции магнитного поля в законе Био-Савара-Лапласа будет равен нулю:
В этом случае \[\vec{r}\] — радиус-вектор, который идет от элемента \[\mathrm{Id\vec{l}}\] к точке А, в которой находится индукция магнитного поля \[\overrightarrow{\mathrm{B}}\].
Индукция бесконечного проводника в точке А была бы равна:
Но так как полу бесконечный проводник, то следуя из принципа суперпозиции, получается следующее выражение для проводника магнитной индукций равна:
Ответ: \[\mathrm{B}=\frac{\mu_{0}}{\pi} \frac{\mathrm{I}}{\mathrm{b}}\]














