Вектор напряженности магнитного поля
Поле моделирует то, что объект испытал бы, связанный с силой в данной точке пространства. Поля часто представляются в двух измерениях с помощью линий поля. Плотность этих силовых линий указывает на напряженность поля в конкретной точке — чем плотнее линии, тем сильнее поле. Условные обозначения того, как отображать линии гравитационного, электрического и магнитного поля, немного отличаются для моделирования уникальных аспектов каждой силы. Некоторые распространенные модели показаны ниже.
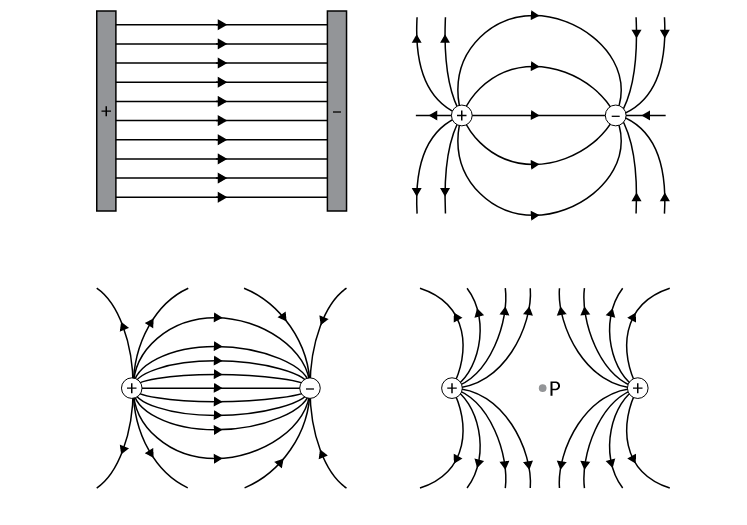
Электрические поля возникают из-за электрических зарядов и изменяющихся магнитных полей. Электрический заряд или совокупность зарядов будут иметь связанное электрическое поле. Любой заряженный объект, помещенный в это поле, будет испытывать электростатическую силу, поскольку поле взаимодействует с зарядом объекта. Силовые линии представляют собой силу, которую испытала бы положительно заряженная частица, если бы она находилась в поле в этой точке.
Изменяющееся магнитное поле также может вызывать перемещение электрических зарядов. Это явление обычно используется в электрических генераторах для наведения электрических токов в проводах. Индуцированный ток можно увеличить, вызывая большие изменения в магнитном поле или сворачивая провод так, чтобы изменяющееся магнитное поле влияло на большее количество проводов.
Определение магнитного поля
Магнитное поле определяется силой, с которой заряженная частица испытывает движение в этом поле, после того как мы учтем гравитационные и любые дополнительные электрические силы, воздействующие на заряд. Величина этой силы пропорциональна количеству заряда q, скорости заряженной частицы v и величине приложенного магнитного поля. Направление этой силы перпендикулярно как направлению движущейся заряженной частицы, так и направлению приложенного магнитного поля. Основываясь на этих наблюдениях, мы определяем напряженность магнитного поля B на основе магнитной силы \[\overrightarrow{\boldsymbol{F}}\] на заряд q, движущийся со скоростью как векторное произведение скорости и магнитного поля, т. е.
Фактически, так мы определяем магнитное поле \[\vec{B}\] — с точки зрения силы, действующей на заряженную частицу, движущуюся в магнитном поле. Величина силы определяется из определения перекрестного произведения, поскольку оно связано с величинами каждого из векторов. Другими словами, величина силы удовлетворяет:
где θ — угол между скоростью и магнитным полем.
Те́сла, единица магнитной индукции (В) в системе СИ, названа в честь физика Н. Теслы. Обозначается Тл.
1 Тл = 1 Н/(А.м)
Иногда используется меньшая единица, называемая гауссом (G), где \[1 G=10^{-4} \mathrm{~T}\].
Напряженность магнитного поля
Напряжённость магнитного поля \[\boldsymbol{H}\] — физическая величина, используемая как
одна из основных мер напряжённости магнитного поля. Единицей напряженности магнитного поля является ампер на метр или А/м.
С инженерной точки зрения напряженность магнитного поля Н можно рассматривать как возбуждение, а плотность магнитного потока В как ответ среды.
С точки зрения теоретической физики поле Н определяется как векторная разность между плотностью потока В и намагничиванием М. Поле H иногда называют «вспомогательным» или просто «полем H».
Эти два подхода идентичны в смысле рассматриваемых физических величин (с одними и теми же физическими единицами А/м), но называются разными именами, и разный акцент делается на их значении и использовании при выводе некоторых уравнений.
Магнитное поле является векторным полем в пространстве и представляет собой вид энергии, полная
количественная оценка которой требует знания векторных полей как напряженности магнитного поля, и плотность
потока (или другие коррелирующие с ними значения, такие как намагниченность M или поляризация J). В вакууме
в каждой точке и векторы ориентированы в одном направлении и прямо пропорциональны через проницаемость
свободного пространства, но в других средах они могут быть смещены (особенно в неоднородных или анизотропных
материалах). Связь между магнитным полем В и напряженностью магнитного поля Н определяется формулой:
\[\boldsymbol{\vec{H}=\frac{\vec{B}}{\mu_{0}}-\vec{M}}\]
Где:
- \[\vec{M}\] = намагниченность материала
- \[\mu_{0}\]= магнитная проницаемость пространства (константа = \[1,25663706 H_{/} A^{2}\])

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Физический смысл напряженности магнитного поля
В вакууме или при отсутствии среды, способной намагничиваться (например, в воздухе), напряженность магнитного поля совпадает с вектором магнитной индукции в пределах коэффициента \[\mu_{0}\]. В способных к намагничиванию средах (магнитах) напряжение носит смысл своеобразного «внешнего поля». Он совпадает с вектором магнитной индукции, каким он был бы, если бы не было магнита.
Циркуляция вектора напряженности магнитного поля
Существует теорема о циркуляции магнитного поля. Это одна из основных теорем электродинамики, сформулированная Анри Ампером. Ее также иногда называют теоремой или законом Ампера. Теорема о циркуляции магнитного поля является своего рода аналогом теоремы Гаусса о циркуляции вектора напряженности электрического поля.
Теорема о циркуляции магнитного поля
Интеграл по замкнутому пути составляющей магнитного поля, касательной к направлению пути, равен \[\boldsymbol{\mu_{0}}\],
умноженному на ток, перехваченный областью внутри пути — теорема о циркуляции магнитного поля,
сформулированная Анри Ампером, которая является своего рода аналогом теоремы Гаусса о циркуляции вектора
напряженности электрического поля.
\[\boldsymbol{\oint \vec{B} \mathrm{~d} \vec{r}=\Sigma I m}\]
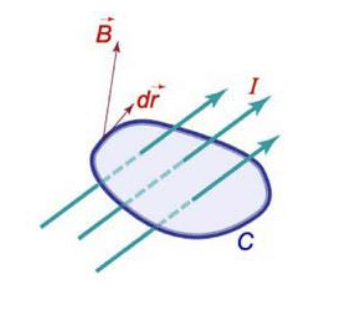
Таким образом, линейный интеграл (циркуляция) магнитного поля вокруг некоторой произвольной замкнутой кривой пропорционален общему току, заключенному в этой кривой.














