Кинетическая и потенциальная энергии
Энергия – одна из ключевых категорий механики. В повседневной жизни мы чаще всего сталкиваемся с механической энергией.
Кинетическая и потенциальная энергия тела
Энергия представляет собой физическую величину, характеризующую способность тела к выполнению работы.
Механическая энергия может быть потенциальной и кинетической. В данной статье мы расскажем о каждом из этих видов, разберем примеры кинетической и потенциальной энергии.
Сумма этих двух видов энергий является постоянной величиной, известной как полная механическая энергия системы, находящаяся в поле сил консервативного типа:
\[E_{К}+E_{П}=E_{M}\]
При этом максимум:
\[E_{м}=E_{k \max }=E_{\text {пmax }}=4 \text { Дж }\]
Кинетическая энергия
Каждое движущееся тело, наделено кинетической энергией. Когда объект пребывает в состоянии покоя этот показатель равен нулю. На него влияет масса тела (m) и скорость (v) перемещения.
Для вычисления кинетической энергии применяют формулу:
\[E_{k}=A=\frac{m v^{2}}{2}\]
Кинетическая энергия (Ек) находится в прямой пропорциональной зависимости от массы и квадрата скорости тела.
Скорость тела, движущегося под воздействием определенных сил, изменилась с \[\vec{v}_{1}\] на \[\vec{v}_{2}\]. Это говорит о том, что этими силами была совершена конкретная работа A.
Работа комплекса сил, оказывающих воздействие на тело, равна по значению той работе, которую совершает равнодействующая сила.
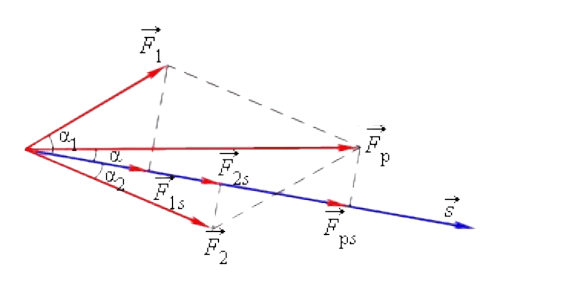
\[\vec{F}_{p}=\vec{F}_{1}+\vec{F}_{2}\]
\[A=F_{1} \cdot s \cdot \cos \cos \alpha_{1}+F_{2} \cdot s \cdot \cos \cos \alpha_{2}\]
Определим взаимозависимость увеличения или уменьшения скорости тела и работы, совершаемой силами, воздействующими на объект.
Представим, что тело движется под воздействием одной силы \[\vec{F}\], направленной вдоль определенной прямой. Сила действует на тело таким образом, что его движение становится равноускоренным и прямолинейным.
Таким образом направление векторов \[\vec{F}, \vec{v}, \vec{a}, \vec{s}\] является одинаковым. Следовательно, эти значения можно представить в качестве алгебраических величин.
\[A=F S\]
Перемещение тела можно выразить формулой:
\[S=\frac{v_{2}^{2}-v_{1}^{2}}{2 a}\]
Исходя из этого:
\[\begin{gathered}
A=F s \cdot \frac{v_{2}^{2}-v_{1}^{2}}{2 a}=m a \cdot \frac{v_{2}^{2}-v_{1}^{2}}{2 a} \\
A=\frac{m v_{2}^{2}-m v_{1}^{2}}{2}=\frac{m v_{2}^{2}}{2}-\frac{m v_{1}^{2}}{2}
\end{gathered}\]
Это подтверждает предположение, что работа, совершенная под воздействием силы, прямо пропорциональна изменения значения квадрата скорости движения тела.
Теорема об изменении кинетической энергии
Опираясь на ранее приведенный пример, сформулируем теорему об изменении кинетической энергии тела, совершающего движение.
Работа, произведенная в результате воздействия силы на определенное тело, эквивалентна изменениям его кинетической энергии. Это утверждение абсолютно применимо и к ситуации, когда на движущееся тело оказывается действие силы, с изменяющимся направлением и модулем.
\[A=E_{k 2}-E_{k 1}\]
Исходя из этого можно резюмировать, что показатель кинетической энергии тела с определенной массой(m), совершающего движение со скоростью \[\vec{v}\], соответствует значению работы, которую сила производит для разгона тела до данной скорости.
\[A=\frac{m v^{2}}{2}=E_{k}\]
Остановка тела потребует совершения работы:
\[A=\frac{m v^{2}}{2}=-E_{k}\]
Потенциальная энергия
Помимо кинетической энергии, которая представляет собой энергию движения существует потенциальная энергия. Она присуща телам, обладающим потенциалом к совершению работы, взаимодействию друг с другом. Поднятое над Землей тело обладает потенциалом к взаимодействию с гравитационными силами. Чем больше оно отдаляется от поверхности, тем сильнее возрастает потенциальная энергия. Если кинетическая энергия зависит от скорости и массы, потенциальная энергия обусловлена взаимным расположением объектов или их частей.
Во время падения тела, сила тяготения совершает работу, на которую влияет только начальное и конечное положение движущегося объекта. Форма траектории значения не имеет. Если она замкнутая, значение работы потенциальной силы будет равным нулю. Среди потенциальных сил можно выделить силу тяготения, упругости и др. Еще их называют консервативными. При упругой деформации тело наделяется энергией взаимодействия между его разными частями.
При перемещении тела вверх, работа силы тяжести будет иметь отрицательное значение.
Подробно разберем пример с вертикальным перемещением шара из точки высота, которой обозначена \[h_{1}\] на отметку с высотой с \[h_{2}\].
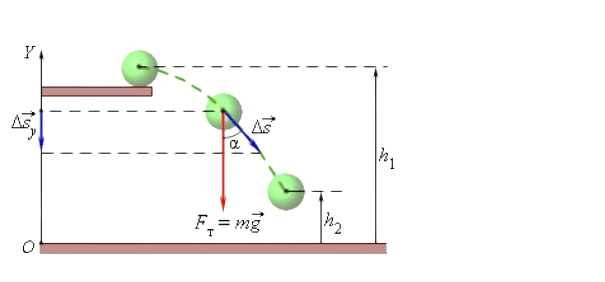
Работа, совершенная силой тяжести равна отрицательному значению \[m g h\]:
\[A=-m g\left(h_{2}-h_{1}\right)=-\left(m g h_{2}-m g h_{1}\right)\]
В следующем примере происходит перемещение тела по наклонной поверхности. Во время движения вниз, на него действует сила тяжести F равная mg. Работа, совершаемая этой силой равна:
\[A=m g s \cos \cos \alpha=m g h\]
В данной формуле, h служит для обозначения высоты наклонной плоскости, S – модуля перемещения, равного длине этой плоскости.

В следующем примере рассмотрим перемещение объекта из точки B в точку C по траектории любой формы. Тело движется по фрагментам наклонной плоскости, с разными высотами \[h^{\prime}, h^{\prime \prime}, h^{\prime \prime \prime}\] и т.д. Работа A представлена в виде суммы работ, совершаемой силой тяжести на каждом из участков пути.
\[\begin{aligned}
&A=m g h^{\prime}+m g h^{\prime \prime} \ldots+m g h^{n}=m g\left(h^{\prime}+h^{\prime} \ldots+h^{n}\right) = m g\left(h_{1}-h_{2}\right)
\end{aligned}\]
\[h_{1}\] и \[h_{2}\] являются высотами относительно земной поверхности, на которых находятся точки B и C.
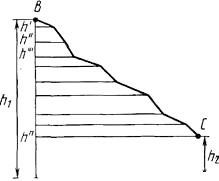
Равенство демонстрирует нам отсутствие влияния траектории пути, по которому движется тело, на работу силы тяжести. Если объект перемещается вниз, значение работы, выполняемой силой тяжести будет положительным, в противном случае – отрицательным. Тогда равенство будет выглядеть следующим образом:
\[A=-\left(m g h_{2}-m g h_{1}\right)\]
На какой высоте кинетическая энергия равна потенциальной
Тело подброшено вверх со скоростью 10м/с. На какой высоте кинетическая энергия предмета будет равна потенциальной?
Определим показатель высоты исходя из того, что:
\[\frac{m v^{2}}{2}=m g h\]
Это значит:
\[h=\frac{v^{2}}{4 g}=\frac{(10 м / c)^{2}}{4 \cdot 10 м / c^{2}}=2,5 м\]
Как изменяются потенциальная и кинетическая энергия тела при падении груза на землю
Для того, чтобы узнать как изменяется кинетическая и потенциальная энергия при падении груза на земную поверхность, рассмотрим свободно падающий камень с высоты h. За счет падения груз набирает скорость v.
Соотношение этих величин при равноускоренном движении:
\[\frac{v^{2}}{2}=g h\]
Каждую из сторон равенства нужно умножить на массу движущегося груза m:
\[\frac{m v^{2}}{2}=m g h\]
Значения кинетической и потенциальной энергии падающего камня взаимозависимы. Последняя уменьшается пропорционально росту первой. Согласно закону о сохранении и превращении энергии, при отсутствии сил сопротивления, механическая энергия, которая является суммой потенциальной и кинетической, остается неизменной. При падении груза происходит переход потенциальной энергии в кинетическую, а после соприкосновения с землей во внутреннюю энергию тела. Температура тела при этом увеличивается.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как влияет скорость на кинетическую энергию и высота на потенциальную энергию
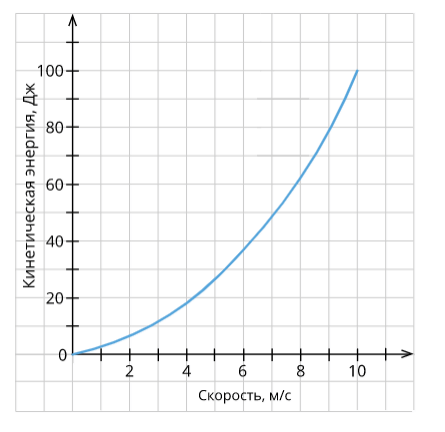
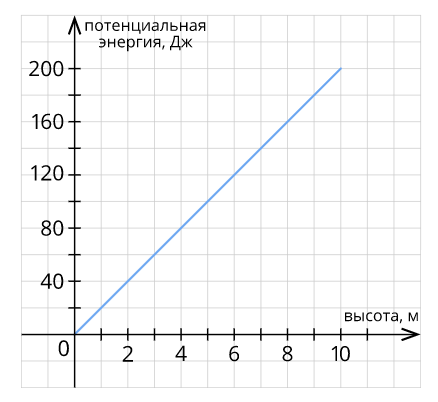
Если скорость движения вырастает вдвое, то кинетическая энергия увеличивается в 4 раза. График демонстрирует зависимость кинетической энергии от скорости. Потенциальная энергия увеличивается пропорционально росту высоты.
Потенциальная энергия пружины
Тело, деформированное в рамках упругой деформации, возвращается к исходному состоянию после удаления силы воздействия. В этот момент объект совершает работу. Упругим телом может служить пружина или резиновый жгут.
Упруго растянутая пружина обладает прямо пропорциональной энергией по отношению к коэффициенту ее жесткости (k) и квадрату значения ее абсолютной деформации \[\Delta \chi\].
Для определения потенциальной энергии пружины с упругим растяжением применяется формула:
\[E_{п}=\frac{k \cdot \Delta x^{2}}{2}\]
От степени жесткости пружины зависит величина ее потенциальной энергии при равном растяжении. Значение \[E_{\text {п}}\] возрастает в 2 раза, когда используется пружина или резинка с увеличенным вдвое коэффициентом жесткости. Сила растяжения влияет на рост потенциальной энергии вне зависимости от жесткости деформируемого объекта. При растяжении пружины в 2 раза энергия увеличивается в 4 раза.
Мысленно представим, две пружины. Одну удлинили на значение x. Вторую вначале растянули на \[2 x\], после чего сжали на x. И в первом и во втором случаях пружину удлинили на x, но к итоговому результату шли разными путями. Значение работы силы упругости при деформировании пружины 1 и 2 способом оказалось одинаковым:
\[A_{упр}=-A=-\frac{k x^{2}}{2}\]
Потенциальная энергия сжатой пружины: \[E_{y п p}=-\frac{k x^{2}}{2}\]
\[E_{\mathrm{ynp}}=-\frac{k x^{2}}{2}\] равна значению работы, совершаемой силой упругости во время перехода пружины из сжатого состояния к первоначальному виду.














