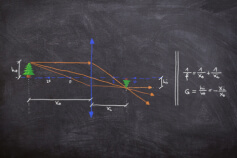
Примеры решения матриц с ответами

2 562

31 октября 2022 г.

Время чтения: 6 минут

Содержание:

Определитель матриц второго и третьего порядка
Вычитание матриц
Умножение матриц
Обратная матрица

Определение

Матрица — это математическая таблица с числовыми значениями. Обозначаются матрицы латинскими знаками.

Есть два вида матриц:

Комплексные матрицы. Одно из чисел равно комплексному.
Действительные матрицы. Матрица в которой содержаться действительные числа.

С матрицей выполняют самые простейшие действия: умножение, деление, сложение, вычитание и трансформацию. Данные действия можно совершать тогда, когда матрицы схожи меж собой, чтобы в самом конце вышло выражение схожей размерности. Сложение и вычитание производятся подобно друг другу.

Эти числа, являются элементами матрицы.

Матрицу можно записать в следующем виде:

\[A=\left(a_{\mathrm{ij}}\right)=\left\|a_{i j}\right\|\]

Квадратная матрица — это число строк, которое равно числу столбцов (m=n), при этом число n – это порядок матрицы.

Пример квадратной матрицы 3-го порядка:

\[A=\left(\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right)\]

Главная диагональ квадратной матрицы – это диагональ, которая состоит из a₂₁,a₂₂, a₂₃, идущая из левого верхнего угла этой матрицы в правый нижний угол. Побочной диагональю квадратной матрицы называется диагональ, составленная из элементов идущая из правого верхнего угла этой матрицы в левый нижний угол.

В квадратной матрице, у которой все элементы, стоящие выше или ниже главной диагонали, равны нулю, называют треугольной, пример:

\[\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{array}\right)\]

Квадратная матрица, у которой все элементы, стоящие на верхней и нижней грани, равны нулю, является диагональной:

\[a_{i} \neq 0, a_{i j}=0\]

Для того чтобы получить квадратную диагональную матрицу с единичными элементами, нужно использовать букву E. Например, квадратная диагональная матрица 3-го порядка имеет такой вид:

\[E=\left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right)\]

Трансформированием квадратной матрицы называется такое преобразование, при котором ее строки становятся столбцом с теми же номерами, а столбец — строкой.

Матрицу, транспонированную по отношению к матрице A, обозначают А^T.

Например, А^T для матрицы А¹ имеет вид:

\[A^{T}=\left(\begin{array}{lll} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{array}\right)\]

Матрица называется нулевой, если все ее элементы равны нулю.

Матрицы А и В называются равными, если они имеют одинаковую размерность, и все их соответствующие элементы совпадают.

Определитель матриц второго и третьего порядка

Определителем второго порядка квадратной матрицы называется число, равное:

\[ A=\left(\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right) \quad \Delta=|A|=\operatorname{det} A=\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|=a_{11} a_{22}-a_{12} a_{21} \]

Суммой А + В двух матриц А=(а_ij) и В= (b_ij) одинакового размера m*n, называется матрица C=(c_ij), элементы которой c_ij=a_ij+ b_ij, для всех i=1,2,…,m и j=1,2…,n.

Задача

\[ \left(\begin{array}{rrr} 1 & 4 & 3 \\ 8 & -3 & 2 \end{array}\right)+\left(\begin{array}{rrr} 3 & 1 & 1 \\ 4 & -1 & 0 \end{array}\right)=\left(\begin{array}{rrr} 4 & 5 & 4 \\ 12 & -4 & 2 \end{array}\right) \]

Согласно правилу сложения матриц A+O=A, где A — произвольная матрица, а O — нулевая матрица того же размера, что и A.

Вычитание матриц

Разность двух матриц одинакового размера определяется с помощью операции умножения матрицы B на число —1 и последующего сложения матриц A и (—1) B т. е.

\[A-B=A+(-1) B\]

Некоторые свойства, присущие операциям над числами, справедливы и для операций над матрицами. В частности, из определений операций умножения матрицы на число и сложения матриц следует, что

\[A+B=B+A\]

Вышеуказанная формула показывает свойство коммуникативности при сложении матриц.

Доказательство. Так как операция сложения определена только для матриц одинакового размера, причем сумма матриц является матрицей того же размера, что и слагаемые матрицы, то очевидно, что размер матрицы

\[A+B=F\]

равен размеру матрицы

\[B+A=G\]

Докажем, что и все элементы матрицы F равны соответствующим элементам матрицы G. Из определения суммы двух матриц следует, что:

\[f_{i j}=a_{i j}+b_{i j}=b_{i j}+a_{i j}=g_{i j}\]

\[\text { для всех } i=1,2, \ldots, m \text { и } j=1,2, \ldots, n \].

Согласно определению равенства матриц, это означает, что:

\[F=G, \text { т. е. } A+B=B+A\]

Умножение матриц

Умножение матрицы на матрицу определено, лишь когда число столбцов первой матрицы в произведении равно числу строк второй.

Произведением двух матриц А и В называется матрица С, элемент которой, находящийся на пересечении i-й строки и j-го столбца, равен сумме произведений элементов i-й строки матрицы А на соответствующие (по порядку) элементы j-го столбца матрицы В. Произведение матрицы А на матрицу В обозначается АВ.

\[c_{i j}=a_{i 1} b_{1 j}+a_{i 2} b_{2 j}+\ldots+a_{i k} b_{k j}=\sum_{s=1}^{k} a_{i s} b_{s j}\]

\[i=1,2, \ldots, m \text { и } j=1,2, \ldots, n .\]

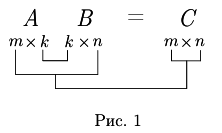
Обратим внимание на размеры матрицы C, число строк матрицы-произведения совпадает с числом строк первой, а число столбцов — с числом столбцов второй из перемножаемых матриц (см. Рис. 1).

Пример. Вычислить произведение матриц AB, если

\[ A=\left(\begin{array}{rrr} 1 & 2 & 3 \\ 5 & 4 & -5 \end{array}\right), \quad B=\left(\begin{array}{rrr} 1 & 2 & 4 \\ 3 & -3 & 1 \\ 1 & 0 & 2 \end{array}\right) \]

Решение матриц:

Определим размер матрицы — произведения:

\[\underset{2 \times 3}{A} \underset{3 \times 3}{B}=\underset{2 \times 3}{C} .\]

Далее, вычислим элементы матрицы — произведения:

\[ C=\left(\begin{array}{rrr} 1+6+3 & 2-6+0 & 4+2+6 \\ 5+12-5 & 10-12+0 & 20+4-10 \end{array}\right) =\left(\begin{array}{lll} 10 & -4 & 12 \\ 12 & -2 & 14 \end{array}\right) \]

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Обратная матрица

Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами.

На рисунке представлен метод решения обратной матрицы:

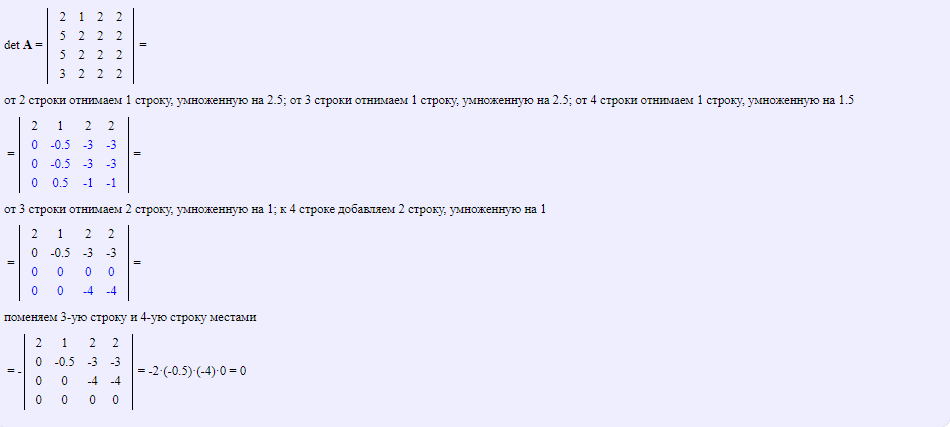
Для вычисления матрицы приведем ее к верхнетреугольному виду, используя преобразования над строками матрицы и свойства определителя матрицы.

По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.

Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.

Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:

Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2.

На первом этапе выполняют действия:

Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.

2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках. При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица: