Деление десятичных дробей
Принцип деления десятичной дроби на простое натуральное число
Для начала дадим определение десятичной дроби.
Десятичная дробь — это число, которое после запятой имеет характерный числовой остаток.
Десятичная дробь – это форма записи обыкновенной дроби, у которой знаменатель равен 1010, 100100, 10001000 и т.д.
Деление десятичных дробей процесс, который представляет собой характерный способ деления обыкновенных дробей. Данные дроби получаются путем преобразования, а именно, переписывание десятичной дроби в стандартный, первоначальный вид.
Примеры десятичных дробей: 145,14; 12,85; 1,23.
В свою очередь данный вид дробей подразделяется на следующие категории:
- Конечные — если после запятой присутствует окончательное число.
Например: ±a0a1a2a3…..an
- Бесконечные — количество цифр после запятой, не имеют окончательного значения, то есть они бесконечны.
Например: ±a0a1a2a3
Основные свойства дробей
Изменение величины десятичной дроби не произойдет, даже если к ней добавить справа несколько нулей. Это свойство принято считать одним из самых главных, для данного вида дробей.
Если в рассматриваемом дробном значении наблюдается множество нулевых значений, тогда их просто исключают, так как никакого влияния на значение они не имеют.
Рассмотрим несколько простых и понятных для ознакомления примеров решения данных дробей:
- 0,900 = 0,9;
- 22,10200000 = 22,102;
- 0,45000=0,45;
- 0,12569000=0,12569;
- 0,780=0,78.
Основные характеристики десятичных дробей
- Дробное число, не будет иметь какого либо значения, если в знаменателе нулевое число. Деление на ноль в математике строго запрещено.
- Нулю будет равна дробь, у которой в числителе значится нулевое значение. В знаменатель — нет.
- Если значения, которые находятся в числителе и знаменателе разделить или перемножить на любое действительное число. То получится дробь равная ей по значении.
- Если взять две дроби.
Алгоритм деления десятичной дроби на простое натуральное число при помощи столбика
Использовать столбик можно не только при делении натуральных простых чисел, а также и при решении дробных числовых значений.
Подробный алгоритм деления для десятичных дробей методом столбик:
1. Для начала нужно прибавить к десятичной дроби несколько нулей справа. Количество нулей принимается в зависимости от делителя.
2. Затем выполняется деление по стандартному методу, как и простые дроби.
3. Следовательно, после того, как деление целой дробной части закончится, нужно поставить знак запятой. Запятая ставится в полученном значении частного.
4. После проведенных вычислений, полученный ответ может выглядеть как конечная или бесконечная дробь.
- Окончательный ответ при делении зависит от значения остатка:
- остаток в виде нулевого значения — ответ будет считаться конечным дробным числом;
- повторение остатка — периодическая дробь.
Существующая взаимосвязь между дробями различных категорий и видов.
- Целая часть десятичной дроби всегда будет равной такой части дроби, только смешанного типа;
- Когда значение в числителе меньше значения знаменателя, то нулю равна целая часть дроби;
- Количество значений после запятой, зависит от количества нулей, которые записаны в знаменателе обыкновенной дроби.
Пример №1:
- Рассмотрим пример деления разделим 4,8 на значение равное 2:
- Распишем пример в виде столбика:
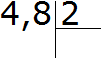
- Затем выполним деление целой части на 2. То есть число четыре разделить на значение равное двум и получим ответ — два. Для этого число 4 нужно записать в частном, поставив при этом знак запятой
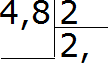
- Далее умножаем значение частного на делитель. Также необходимо выяснить, есть ли остаток от деления
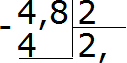
- Так как 4−4=0, следовательно, остаток будет нулевой. Решение примера не завершено, поэтому остаток не записывается.
- Решение продолжаем, используя принцип обычного деления:
- Для этого число 8 опускается и делится на 2.
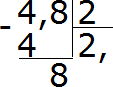
Пример № 2:
- Вычислить значение заданного примера:8,43 : 3
- Разделим 8 на 3 и получим ответ 2 и необходимо поставить знак запятой после цифры 2:
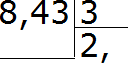
- Затем умножаем значение частного на делитель, а именно 2 × 3 = 6. Число шесть записывается под числом восемь и определяется остаток:
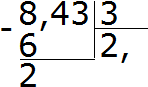
- Далее пример решается как обычное деление. Определяется ответ и число четыре сносится:
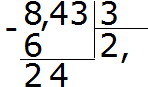
- При делении 24 на три получаем ответ 8. Полученное значение равное восьми записывается в частном. Затем умножаем его на делитель и определяем остаток от выполненного деления:
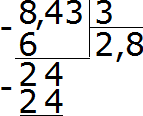
- Так как 24−24=0 следовательно, и остаток равен нулю. Последнее значение три сносится из делимого и делится на него. Окончательный ответ получается один. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
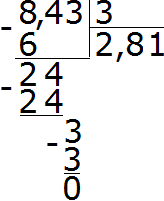
Ответ задачи: 8,43 : 3 = 2,81
Деление десятичной дроби на десятичную дробь
Чтобы выполнить деление десятичной дроби на аналогичную дробь, необходимо делимое и делитель преобразовать, так:
- чтобы запятая вправо сместилась на количество цифр, сколько их имеется после запятой в делителе;
- выполнить деление на простое действительное число.
Пример №1:
Выполним деление 5,95 на 1,7
Применяя уголок, запишем выражение: 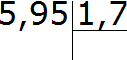
Далее, необходимо в делимом значении и в делителе перенести запятую. Перенос необходимо сделать в вправо на количество цифр, равное количеству их после запятой в значении делителя.
Так как в делителе после запятой имеется одна цифра, значит нужно в делимом и делителе запятую перенести в вправо только на одну цифру. Выражение будет иметь следующий вид: 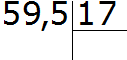
После того, как запятая меняет свое расположение, в вправо на одно значение, десятичная дробь равная 5,95 будет выглядеть следующим образом: 59,5.
После переноса в право знака запятой, десятичная дробь равная 1,7 будет выглядеть как простое натуральное число равное 17.
Используя, уже известный алгоритм решения для десятичных дробей, можно выполнить последующее решение: 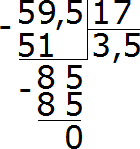
Перенос запятой необходим, для простоты решения.
Данный способ применяется по причине того, что при выполнении умножения или деления, значения делимого и делителя не изменяются, при условии одинакового числа.
Это и является одной из важных особенностей процесса деления.
Данное свойство — это свойство частного при делении.
Пример №2:
Рассмотрим подробно следующее выражение: 9: 3 = 3.
Если в данном примере значение делимого и делителя умножить или разделить на одинаковое число, тогда значение частного равное 3 не будет изменяться.
При перемножении делимого и делителя на значение равное двум получим следующее решение:
(9 × 2) : (3 × 2) = 18 : 6 = 3
Если внимательно посмотреть выражение, то можно сделать вывод, что значение частного не изменилось.
Аналогичный вид будет иметь пример, в случае, когда производится перенос запятой в делимом и в делителе.
В вышеприведенном примере, был произведен расчет деления 5,91 на 1,7. В делимом и делителе была перенесена запятая на одно числовое значение вправо.
Когда переносится запятая, дробь равная значению 5,91 преобразовывается в дробь 59,1 а значение дроби 1,7 изменяется в обычное натуральное число равное 17.
Иными словами, в данном случае выполнялось умножение значений на 10.
В виде примеров, это выглядит следующим образом:
5,91 × 10 = 59,1
1,7 × 10 = 17
Количества значений после знака запятой в делителе, всегда будет зависит от, значения на которое будет умножено значение делителя и делимого.
То есть количество цифр после запятой в обоих случаях зависит от того, насколько цифровых значений будет перенесен знак запятой.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Способы деления десятичной дроби на числа 10, 100, 1000
Процесс деления значений десятичной дроби на числа 10, 100, или 1000 происходит таким же образом, как и все остальные способы, связанные с делением дроби данного вида.
Пример №1:
Выполним деление значений 2,1 на число 10. Решение будет проводится при помощи разложения чисел в виде уголка: 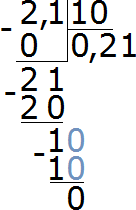
Однако, можно использовать иной способ для решения данного примера:
Именно этот способ является наиболее простым и легким.
Основное правило при решении, состоит в том, что:
- знак запятой в делимом перемещается влево на количество цифр, равное количеству нулей в значении делителя.
Исследуя делитель, определяем количество нулевых значений в нем. Так как в нем имеется один нуль, то в делимом равным 2,1 необходимо перенести знак запятой влево на одно значение.
После перемещения запятой влево на одно цифровое значение. Можно сделать вывод, что цифр больше не осталось.
Поэтому, нужно перед цифрой добавить ещё одно нулевое значение.
После данных операций и преобразований получаем следующее значение равное 0,21:
2,1: 10 = 0,21
Выполним деление десятичной дроби равной 2,1 на значение равное 100.
Так как в числе 100 присутствует два нуля, соответственно в делимом 2,1 нужно поставить знак запятой влево на два значения:
2,1: 100 = 0,021
Аналогично выполним деление числа 2,1 на значение равное 1000.
Значение 1000 имеет три нуля. Поэтому в делимом равным 2,1 нужно перенести знак запятой влево на количество цифр равным трем:
2,1: 1000 = 0,0021.
Особенности деления десятичной дроби на следующие значения равные 0,1, 0,01 и 0,001
Принцип деления десятичных дробей на числовые значения равные 0,1; 0,01; 0,001, происходит по методу, как алгоритм деления десятичной дроби на подобную.
Для этого необходимо в делимом значении и делителе перенести знак запятой. Запятая перемещается вправо на количество цифр равным их количеству, после запятой в делителе.
Пример №1:
Выполним деление числового значения равным 6,3 на число 0,1.
- Первым действием необходимо перенести запятую в делимом значении и делителе в правую сторону. А именно: на определенное количество чисел, которое равняется количеству значений после знака запятой.
- Так как делителе имеется после запятой только одна цифра. Далее, необходимо перенести запятую на одну цифру, как в делимом, так и в делителе.
- После, того как выполнено действие по переносу запятой, на одно значение, десятичная дробь равная 6,3 преобразуется в простое натуральное число равное 63. Десятичная дробь равная 0,1 соответственно будет равна единице, после переноса знака запятой вправо.
- Нужно выполнить деление 63 на значение равное 1:
63 : 1 = 63
Из этого следует, что значение примера 6,3 : 0,1 равно числу 63:
6,3 : 0,1 = 63
Принцип деления десятичной, обыкновенной дроби на дробное десятичное значение или в обратном порядке
Данное действие также сводится к простым операциям, связанным с обыкновенными дробями:
- Для выполнения данного решения необходимо десятичные дроби заменить на обыкновенные. Если присутствуют смешанные числа, то их следует заменить на неправильную дробь.
- Если нужно разделить непериодическую дробь на дробь обыкновенного вида или на смешанное число. В данном случае нужно все действия выполнить наоборот. Для этого необходимо поменять простое значение дроби. Либо значение в виде смешанного числа на дробное десятичное значение соответствующего вида.















