Сокращение дробей: правила и примеры
Самые старые упоминания о таких математических явлениях, как дробь, учёные обнаружили в древнем Египте. Особенностью их было то, что у них были обозначения только вида 1\2, 2\3,1\3, при этом больше двойки числа, делимого они не использовали, а использовали метод сложения, к примеру, вместо дроби 5\6, писали 1\2 +1\3.
Но применять такие дроби было сложно, поэтому учёные разных областей пытались вывести общую универсальную формулу для удобства. Так появилась шестидесятеричная, но проводить вычисления с ней тоже было очень трудно, однако её довольно долго применяли в Вавилоне и Греции. Существовала также система называемая Асс, её суть в делении на 12, использовали её римляне. Результат такого деления, точнее одну долю, называли унцией. Самой близкой по своей системе исчисления была дробь, которую предложили в Индии, разница от современных была в формате записи, без чёрточки, и такая дробь была перевернута, в верхней части находился делитель, а в нижней делимое. Та запись, которую и по сей день используют в математике была придумана арабами.
Что такое дробь, основные понятия и виды
Дробь — число, состоящее из нескольких равных долей.
По сути дробь — это деление одного числа на другое. Выделяют два вида: обыкновенные и десятичные.
Обыкновенная дробь — означает, состоящая из целых чисел. Обыкновенные, имею два типа записи к примеру:
- 1\5- разделена наклонной линией, читается как одна пятая;
- \[\frac{1}{5}\] — горизонтальной линией.
Определения:
- Числитель — число, находящееся в верхней границе дроби;
- Знаменатель — число которое мы видим в нижней границе дроби.
Например: 1\5, где 1- числитель, 5- знаменатель. Для того чтобы проще объяснить, что такое дробь приведём простой пример. Торт разрезан на 5 кусков, если мы взяли два и них то это 2\5 (две пятые части торта).
Обыкновенные дроби имеют два типа правильные и неправильные.
Правильной дробью называется дробь с значениями, в которых числитель меньше знаменателя. Такое название данный тип дроби получил не зря, ведь так логичнее и правильнее, когда часть меньше целого.
Неправильная в свою очередь имеет обратные значения, когда числитель больше знаменателя.
Примечание. Дроби, у которых знаменатель и числитель одинаковы, тоже неправильные.
Смешанная дробь. Существует также такое определение как смешанная дробь, такой вид, представляет собой дробь, состоящую из двух частей целой и дробной. Пример — \[4 \frac{3}{5}\], где четыре это целая часть, а 3\5 дробная. Такой тип дроби можно получить, только при делении неправильного вида дробей.
Десятичные дроби. К десятичным, относят дроби которые в знаменателе имеют 10 в натуральной степени. К примеру \[\frac{5}{10}, \frac{6}{100}\] и тд. Такие, так же могут иметь вид строчной записи, 0,5 и 0,06. При этом в такой записи целая часть отделяется от дробной знаком запятой.
Существуют также понятия сократимой и несократимой дроби. Сократимая дробь, это та, в которой можно произвести деление числителя и знаменателя на одно и то же число.
Несократимая дробь, если такие действия выполнить нельзя.
Составная дробь, многоуровневая или выражение, имеющее несколько черт дроби. Пример \[\frac{\frac{3}{7}}{-31}\]
Равные и неравные дроби. Для того чтобы сказать, являются дроби равными или нет, нужно их сравнить.
Равные обыкновенные \[\frac{a}{d} \frac{c}{b}\] — можно вывести при помощи такого верного равенства а*b=d*c , если такое равенство не верно то данные дроби будут называться неравными.
Положительные и отрицательные дроби.
Положительные называют обыкновенные дроби, с положительными числами, при необходимость перед такими дробями ставится знак +, пример \[+\frac{6}{9}\].
Отрицательными, считаются дроби со знаком минус, пример \[-\frac{6}{9}\].
Стоит отметить что две дроби вида \[-\frac{6}{9} \text { и }+\frac{6}{9}\] являются противоположными.
Алгебраическая дробь.
Отличается она тем, что на месте числителя и знаменателя находятся алгебраические значения, числа заменены буквами. Примеры —
Если в такой дроби буквы заменить числами, то она сразу станет обыкновенной.
Одночлен — это выражение, содержащее числа, степени положительные и их произведение. Пример: ![]() в.
в.
Многочлен — это сумма одночленов. Пример: 7а+6в
Дроби на координате прямых.

Если рассматривать координату прямых, то положительные дроби на ней будут расположены справа от нулевого значения, а отрицательные слева.
Действия, которые можно выполнить с дробями
В общем то, действия с дробями это все те же действия, которые можно выполнить с числами:
- Сравнение;
- Сложение;
- Вычитание;
- Умножение;
- Деление.
Свойства дроби
Чтобы сложить или вычесть дроби, дробь обязана иметь равные знаменатели, необходимо просто выполнить это действие с их числителями
Примеры:
Что же касается дробей с разной частью делителя (Знаменателя), то тут чтобы выполнить действия сложения и вычитания с ними необходимо привести знаменатели к общему числу.
Примеры: \[\frac{4}{9}+\frac{5}{8}=\frac{4+5}{9 \cdot 8}\], точно так же и для вычитания.
Чтобы выполнить такое действие, как умножение обыкновенных дробей, нужно произвести умножение сначала с их числителями, а после и знаменателями.
Пример: \[\frac{4}{9} \cdot \frac{5}{8}=\frac{4 \cdot 5}{9 \cdot 8}\].
При умножении дроби на число, в такой вычислении просто умножается числитель на заданное число, а знаменатель остаётся тем же.
Пример: \[\frac{4}{9} \cdot 6=\frac{4 \cdot 6}{9}\];
Что же касается деления, то при делении одной дроби на другую, нужно произвести умножение, при котором первая дробь остаётся в неизменном виде, а вторая переворачивается. То есть получается мы умножаем числитель первой дроби данного примера, на знаменатель второй, и полученное число находится в верхней части дроби, а в нижней умножение знаменателя первой дроби на числитель второй.
Пример: \[\frac{4}{9} \backslash \frac{5}{8}=\frac{4 \cdot 8}{9 \cdot 5}\].
Сравнение дробей
Чтобы провести сравнение с разными делителями (знаменателями), необходимо сделать так, чтобы знаменатель стал общим только тогда можно будет сравнить числители. Соответственно, где числитель больше там и дробь больше.
Основное свойство дробей
Основным свойством дроби является выражение — «числитель и знаменатель можно делить и умножать на одно и то же число при этом значение всей дроби не поменяется.»
Еще одно определение которое пригодится нам для сокращения дроби это НОД.
НОД — наибольший общий делитель.
Общий делитель — это число, которое может быть делителем каждого из указанных чисел.
Пример: если взять число 3, то оно станет общим делителем для чисел 6 и 9. так как 9=3*3 а 6=3*2.
Алгоритм Евклида для вычисления НОД (наибольшего общего делителя)
Не всегда, сходу, можно понять какое число является наибольшим общим числителем, особенно если числа крупные, поэтому существует специальный алгоритм для выведения такого числа НОД.
Суть алгоритма такова: для нахождения НОД чисел а и b (где они целые и положительные числа, к тому же a больше b), выполняется ряд делений с остатком, получается ряд равенств, где деление останавливается в том случае если rk+1=0, при этом rk=НОД(a, b)
Пример. Рассчитаем НОД для 28 и 64.
Как находим:
Распишем простые множители для каждого числа и подчеркнем одинаковые
Д (28) = 2 * 2 * 7
Д (64) = 2 * 2 * 2 * 2 * 2 * 2
Найдем произведение одинаковых простых множителей и запишем ответ
НОД (28; 64) = 2 * 2 = 4
Ответ: НОД (28; 64) = 4
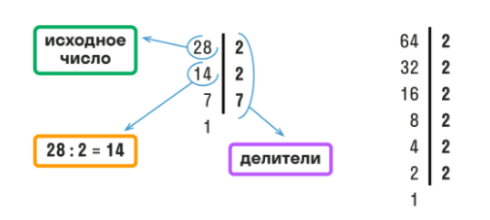
Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.
Сокращение дроби
Выражение сократить дробь, фактически означает что необходимо провести деление её числителя и знаменателя на одно и то же число, не равное единице.
Результатом таких действий станет появление новой дроби, значение которой, равно первичной.
Например: возьмём обыкновенную дробь \[\frac{12}{44}\] и произведем сокращение. Для этого разделим и числитель и знаменатель на 2, получится такая дробь \[\frac{12}{44} \backslash 2=\frac{12 \backslash 2}{44 \backslash 2}=\frac{6}{22}\].

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Несократимый вид дроби, приведение к такому виду
Обычно целью таких манипуляций с дробями является получение из исходного вида дроби несократимый. К примеру дробь, которая получилась у нас выше, \[\frac{6}{22}\] при сокращении на два, как мы видим все ещё можно сократить.
Для того чтобы привести дробь к виду несократимой, нужно выполнить манипуляции по делению, числителя и знаменателя на наибольший НОД. В таком случае по свойству НОД в числителе и знаменателе окажутся простые числа, а дробь будет несократимой.
Из вышесказанного следует, что приведение дроби к несократимому виду значит, нужно произвести деление числителя и знаменателя на их НОД.
Пример: вернёмся к нашему примеру дроби \[\frac{12}{44}\], для приведения ее к несократимому виду нужной сначала найти наибольший общий делитель чисел 12 и 44. таким числом НОД для них является цифра 4.
Получается: \[\frac{12}{44}=\frac{12 \backslash 4}{44 \backslash 4}=\frac{3}{11}\].
Для чего нужно сокращение? Такие манипуляции с дробями необходимо применять, в случаях работы с большими числами.
Стоит вспомнить негласное правило математики, суть его в том, что если что-то можно сделать проще нужно упростить. Поэтому, говоря о сокращении дроби, имеется в виду именно приведение к несократимому виду, а не просто уменьшение числителя и знаменателя.
Правило сокращения
Для того чтобы сократить, необходимо:
- Найти делитель наибольшего значения, который будет общим для знаменателя и числителя;
- Разделить числитель и знаменатель на него.
Примеры:
Дана такая дробь: \[\frac{182}{195}\]. сократим её.
Найдём такой делитель, при помощи применения алгоритма Евклида.
195 = 182 *1+13
182=13*14
Из чего следует, что НОД(182,195)=13
Поэтому для сокращения дроби \[\frac{182}{195}\], разделим числитель 182 и знаменатель 195 на 13 и получим равенство: \[\frac{182}{195}=\frac{182 \backslash 13}{195 \backslash 13}=\frac{14}{25}\]
Таким образом мы и получили несократимую дробь равную исходной.
Второй способ.
Второй способ основан на разложении числителя и знаменателя исходной дроби на простые множители, из которых позже все общие множители убираются.
Пример сокращения: \[\frac{123}{154}\] для сокращения представим числитель и знаменатель дроби в виде простых множителей
Затем уберём все общие множители, как в числителе так и в знаменателе, \[\frac{182}{195}=\frac{2 \cdot 7 \cdot 13}{3 \cdot 5 \cdot 13}=\frac{2 \cdot 7}{3 \cdot 5}=\frac{14}{15}\]
Третий способ сокращения дроби.
Третий способ — способ последовательного сокращения. Применяя такой способ, сокращение происходит поэтапно, сокращая каждый раз на какой-либо очевидный общий множитель.
Пример: \[\frac{18000}{22000}\]
При сокращении такой дроби сразу можно увидеть, что и числитель и знаменатель деяться на 1000 в результате такого деления получается:
Следующим этапом мы видим, что оба значения и числителя, и знаменателя делятся на 2, получим несократимую дробь.
Как мы видим сокращение дроби не такой сложный процесс, главное подобрать удобный способ.
Сокращение алгебраической дроби
Так же, как и в примерах выше, сокращение алгебраической дроби, это деление числителя и знаменателя на общий делитель. Отличие в том, что в алгебраической, таким общим множителем является многочлен и одночлен.
Для того чтобы сократить такие дроби нужно пройти три этапа:
- Определение множителя, который будет общим для числителя и знаменателя;
- Сокращение коэффициента;
- Деление числителя и знаменателя на множитель.
Сокращая дробь со степенями, применяется правило деления степеней с равными основаниями.
Формула:
Рассмотрим пример сокращения со степенями:
Исходя из вышеописанной схемы:
- Сокращаем x3 и x2;
- Производим деление выбирая меньшее значение степени;
- Вычитаем.
В результате получаем сокращенную дробь.
Не забываем, что сократить можно только одинаковые буквенные множители.
Сокращение дробей с одночленами.
Пример: \[\frac{40 x}{5 x^{2}}=\frac{8}{x^{2-1}}=\frac{8}{x}\]
Решение:
- 8 — тот самый множитель, который является общим
- Х и x2 делим на x и получаем ответ.
Дроби с многочленами: сокращение.
Для сокращения таких видов, существует два правила:
- Сократить многочлен в взятый в скобки, можно только с точно таким же многочленом в скобках;
- Сократится должен весь многочлен, взятый в скобки, нельзя сократить только часть.
Пример: \[\frac{x-c}{x(x-c)}=\frac{1}{x}\]
Вынесение общего множителя при сокращении.
Бывают случаи, когда при сокращении алгебраической дроби с многочленами, их нет одинаковых, в таком случае нужно убрать общий множитель за скобки.
Для такого вынесения тоже существуют правила их 4:
- необходимо найти число, на которое можно разделить числа каждого одночлена;
- необходимо также найти буквенный множитель, который повторяется, в каждом одночлене, их может быть несколько;
- выносим буквенный множитель, который был найден, за скобки;
- производим работу с оставшимися многочленами в скобках.
Для того чтобы умножить многочлен на одночлен, необходимо по очереди умножить каждый член многочлена на одночлен.
Приведём пример:
Калькулятор сокращения дробей
Подведём итоги. Для того чтобы не возникло трудностей с сокращением, стоит запомнить:
- Сокращая дробь вам необходимо найти общий множитель для числителя и знаменателя, если речь идет об алгебраических дробях, но и НОД обыкновенных;
- Разделить числитель и знаменатель на общий множитель\делитель;
- Если дробь алгебраическая, при делении многочлена на множитель необходимо вынести общий множитель за скобки;
- Стоит хорошо выучить все формулы и определения, связанные с дробями.
- Всегда проверять результат сокращения.















