Формулы сложения: доказательство, примеры
Базовые формулы сложения тригонометрических функций
Формулы сложения выражают функции суммы углов поворота α и β или их разности, одни из самых используемых формул в тригонометрии.
С помощью тригонометрических формул сложения можно вывести множество прочих важных формул и сделать выражение проще, чем исходное.
- Синус суммы углов α и β определяется следующим образом:
- умножаем синус и косинус углов \[\alpha \text { и } \beta\];
- вычисляем произведение косинуса и синуса этих углов;
- получившиеся значения складываем.
Запись выглядит следующим образом:
\[\sin (\alpha+\beta)=\sin \alpha * \cos \beta+\cos \alpha * \sin \beta ;(1)\]
- Синус разности находят подобным образом. В первую очередь умножаем синус (sin) угла \[\beta\] на косинус (cos) угла \[\alpha\], затем косинус угла \[\alpha\] умножаем на синус угла \[\beta\] и находим их разность. Формула выглядит следующим образом:
\[\sin (\alpha-\beta)=\sin \alpha * \cos \beta-\cos \alpha * \sin \beta ; (2)\] - Косинус суммы вычисляют следующим образом: косинус (cos) угла \[\alpha\] следует умножить на косинус (cos) угла \[\beta\] и синус (sin) угла \[\alpha\] на синус (sin) угла \[\beta\], далее находим их разность. Формула сложения для косинуса cos выглядит так:
\[\cos (\alpha+\beta)=\cos \alpha * \cos \beta-\sin \alpha * \sin \beta;(3)\] - Косинус разности углов α и β вычисляется как сумма произведений косинусов значений углов α и β и синусов углов α и β.
\[\cos (\alpha-\beta)=\cos \alpha * \cos \beta+\sin \alpha * \sin \beta;(4)\] - Тангенс суммы выражается дробным выражением, где в числителе сумма тангенсов углов α и β. Произведение тангенсов углов α и β вычитается из единицы в знаменателе. Запись формулы:
\[\operatorname{tg}(\alpha+\beta)=\frac{\operatorname{tg} \alpha+\operatorname{tg} \beta}{1-\operatorname{tg} \alpha * \operatorname{tg} \beta}\];(5) - Тангенс разности определяется следующим образом. В дробном выражении в числителе указывается разность тангенсов углов α и β, а в знаменателе к 1 прибавляется произведение тангенсов углов α и β.
\[\operatorname{tg}(\alpha-\beta)=\frac{\operatorname{tg} \alpha-\operatorname{tg} \beta}{1+\operatorname{tg} \alpha * \operatorname{tg} \beta};(6)\] - Для вычисления котангенса суммы необходимо найти произведение и сумма сумма котангенсов заданных углов.
\[\operatorname{ctg}(\alpha+\beta)=\frac{-1+\operatorname{ctg} \alpha * \operatorname{ctg} \beta}{\operatorname{ctg} \alpha+\operatorname{ctg} \beta};(7)\] - Котангенс разности определяется схоже с предыдущей формулой, с той разницей, что в числителе и знаменателе дроби ставится минус, а не плюс.
\[\operatorname{ctg}(\alpha-\beta)=\frac{-1-\operatorname{ct} g \alpha * \operatorname{ctg} \beta}{\operatorname{ctg} \alpha-\operatorname{ctg} \beta};(8)\]
Для краткости записи формул сложения чисел, их группируют, с применением знаков плюс/минус \[\pm\] либо минус плюс \[\pm\].
Доказательство формул сложения
Большую часть понятий в алгебре можно доказать. Формулы сложения нужны в старших классах для подготовки к ЕГЭ по математике и имеют свои доказательства. Рассмотрим формулу косинуса разности (4). С ее помощью осуществляется доказательство остальных формул сложения.
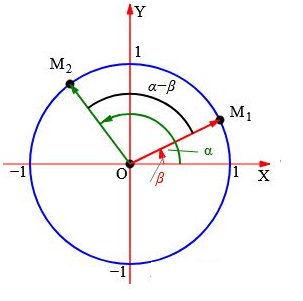
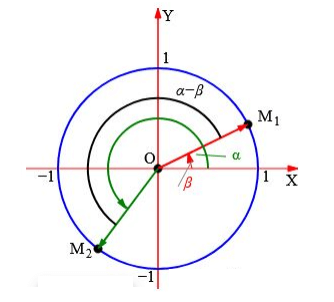
На рисунке 1 положительная часть О – общая начальная точка углов α и β. Точки \[M_{1} \text { и } M_{2}\] отстоят от начала координат на 1. Известно, что угол между векторами не должен превышать 180° (π). Единичная окружность получилась путем поворота точки М вокруг центра О на угол α и β. Угол между векторами \[O M_{1} \text { и } O M_{2}\]. равен α – β. Угол между векторами \[O M_{1} \text { и } O M_{2}\] на рисунке 2 равен \[2 \pi-(\alpha-\beta)\].
Далее проведем анализ косинусов этих углов. С помощью формул приведения вычислим: \[\cos (2 \pi-(\alpha-\beta))=\cos (\alpha-\beta)\]
Скалярное произведение векторов \[M_{1} \text { и } M_{2}\]:
Определение синуса и косинуса говорит, что синус – это функция угла, которая соответствует отношению катета противолежащего угла к гипотенузе. В свою очередь косинус – представляет собой синус дополнительного угла. В связи с тем, что координаты точки \[M_{1}(\cos \beta ; \sin \beta)\]; координаты точки \[M_{2}(\cos \alpha ; \sin \alpha)\]. Вычислим скалярное произведение по координатам векторов \[M_{1} \text { и } M_{2}\]:
На рисунках представлена единичная окружность, соответственно, длины всех векторов равны 1.
Левые части формул (9) и (10) равны, значит, равны и правые части этих выражений. Равенство формулы косинуса разности выполнено.
Как доказать формулу сложения косинусов
Для доказательства формулы (3) воспользуемся предыдущими расчетами. Для этого запишем косинус суммы углов α и β как косинус разности этих углов. Для доказательства формулы сложения используем свойства sin и cos. Косинус функция четная и не меняет знак при смене знака угла (аргумента) \[\cos (-\alpha)=\cos \alpha\], а синус нечетная \[\sin (-a)=-\sin \alpha\]

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Доказательство формулы сложения синусов
Рассмотрим доказательство формулы синуса суммы (1). С помощью формул приведения можно вывести из рассмотренной ранее формулы косинуса разности.
Для доказательства синуса разности (2) рассмотрим разность углов как сумму, для этого используем, что функция косинуса четная, а синуса – нечетная.
Доказательство формулы сложения тангенсов
Тангенс – соотношение синуса к косинусу.
В результате у нас получилась сложная дробь. Затем разбиваем числитель и знаменатель дроби как \[\cos \alpha * \cos \beta\].
Вычисления проводим с учетом того, что \[\cos \alpha \neq 0 \text { и } \cos \beta \neq 0\].
Затем сокращаем дроби, в результате получается следующая формула:
Для доказательства формулы (14) выразим разность углов как сумму. Для этого воспользуемся формуй (6) учитывая, что тангенс нечетная функция:
Доказательство формулы сложения котангенса
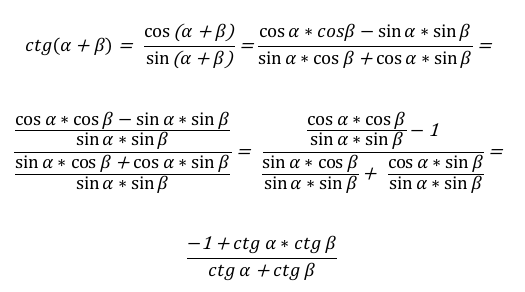
Для доказательства формулы (8) запишем разность углов \[\alpha \text { и } \beta\] как сумму, учитывая, что котангенс нечетная функция:
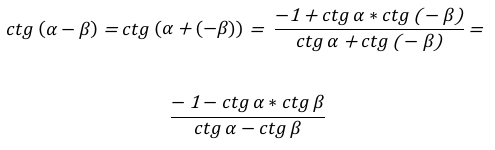
Формулы сложения тригонометрических функций позволяют получать значения новых углов на основе уже известных значений.
К примеру, вычислим sin15°
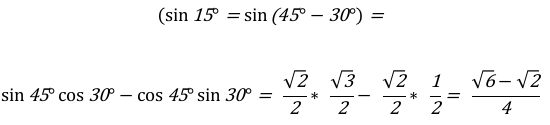
Пример 2. Найти тангенс угла 15°.
Решение:
Значения тангенсов углов 45° и 15° известны. Получаем:
Упрощаем дробь в правой части:
Ответ: \[\operatorname{tg} 15^{\circ}=2-\sqrt{3}\]















