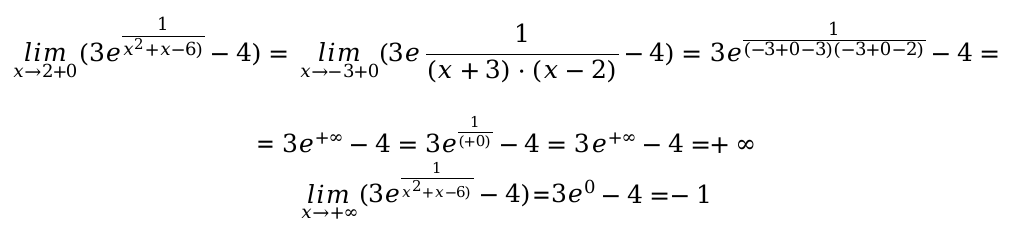Возрастание и убывание функции на интервале, экстремумы
Прежде, чем начать изучение материала, охарактеризуем основное определение значению функции.
Функция — это определенное соответствие между двумя множествами. Функции удобно изображать в виде графических прямых или кривых.
Данная зависимость между x и y в алгебре называют функциональной.
Записывают ее в виде функции y = f(x)
Далее можно сформулировать определение область функции. То есть, на какой промежуток действе функции распространяется.
Область функции можно выразить геометрически. Например, в виде графика. Где за основу берутся оси х и y.
Область определения и ее характеристика
Функция задается тогда, когда любому значению, например x соответствует любое y. Независимой переменной называют значение х или по-другому аргументом. Числовое значение y, как правило, является зависимой переменной.
Данная зависимость между x и y в алгебре называют функциональной. Записывают ее в виде функции y = f(x)
Далее можно сформулировать определение область функции. То есть, на какой промежуток действе функции распространяется.
Область функции можно выразить геометрически. Например, в виде графика. Где за основу берутся оси х и y.
Область ограничения действительных чисел может быть от \[(0;+\infty,)\].
Например: [-4;1)\[U\][5,7).
Область определения может указывать на следующие характеристики:
- деление функции как \[y=x+\frac{2 \cdot x}{x^{4}-1}\];
- корень четной степени и переменная под корнем:
\[=\sqrt{x+1} \text { или } y=\sqrt[n]{2^{2 \cdot x+1}}\];
- переменная в основании степенного значения \[y=3 \cdot(x+1)-2, y=-2+x^{\frac{1}{3}} ; y=\left(x^{4}-x+2\right)^{\sqrt{4}}\]
- логарифмическая переменная \[y=\ln \frac{x^{4}+x}{8} ; \quad y=2+\]. Значения основания должно быть положительным. Также, как и логарифмическое значение.
- переменная тангенса и котангенса в виде следующего уравнения: \[y=\arcsin (x+4)+4 \cdot x^{2}\].
Если отсутствует хотя бы один из перечисленных характеристик область определения функции определяется иначе.
Пример 1: \[y=\frac{x^{4}+2 x-x+2}{4}+2 \frac{2}{3} \cdot x\], в данном множестве нет переменной, поэтому и решается оно иначе.
Пример 2: \[y=\frac{3}{x-1}\], нужно вычислить область определения. Обязательно, при решении нужно уделить внимание на знаменатель. Потому что, по законам алгебры деление на ноль запрещено.
Следовательно получаем следующее действие: \[\frac{3}{x-1}\].
Область не должна быть равной единице, так как в знаменателе получим нулевое значение. Отсюда область определения будет в пределах \[(-\infty, 1) \cup(1,+\infty)\].
Определение значений функции на заданном отрезке
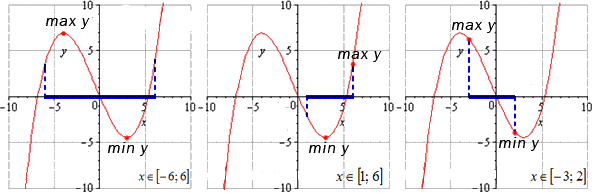
На первом рисунке изображена функция, которая может принимать максимальное и минимальное значение в точках, которые расположены на промежутке (-6;6).
Для примера, рассмотрим второй график. Заменим числовые значения на отрезке (1;6). Максимальное значение функция принимает в соответствующей точке справа.
Третий график показывает функцию, на которой точки являются граничными для отрезка (-3;2). Следовательно, они и соответствуют максимальному и наименьшему значению функции, которая задана.
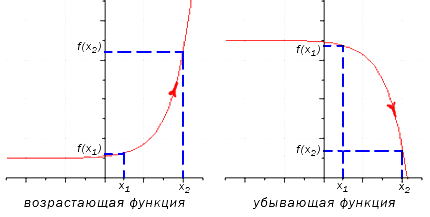
Возрастание и убывание значений функции на промежутке
Любая функция вида: y=f(x) будет возрастать на заданном интервале значений X, при условии, что \[x_{1} \in X_{n} \] и \[\quad x_{2} \in X, \quad x_{2}>x_{1}\] и выполняется следующее неравенство \[f\left(x_{2}\right)>f\left(x_{1}\right)\].
Иными словами – наибольшему значению заданного аргумента соответствует максимальное значение для функции.
При убывающем положении функции будет наблюдаться следующее:
Функция вида: y=f(x) будет убывающей на определенном интервале значений X, если для любых \[x_{1} \in X_{n} \] и \[\quad x_{2} \in X, \quad x_{2}>x_{1}\] выполнимо определенное неравенство.
То есть максимальному значению аргумента будет справедливо наименьшее заданное значение функции.
В случае, когда функция определенная и является непрерывной по значению в концах интервала увеличения или уменьшения (a;b). Следовательно, при значениях x=a и x=b, все заданные точки будут входить в промежуток, где функция будет иметь возрастающий или убывающий вид.
Данное утверждение не противоречит всем определениям возрастания и убывания функции на промежутке значений.
Пример:
Используя свойства основных простых функций известно, что функции y=sinx определенная и непрерывная для всех действительных чисел функции синуса будет возрастать на интервале \[\left(-\frac{\pi}{2} ; \frac{\pi}{2}\right)\].
Экстремум точки для функции
Точка максимума для значения функции — это точка \[x_{0}\] для функции y=f(x), при правильности неравенства данных \[f\left(x_{0}\right) \geq f(x)\] для любых применяемых значений \[x\].
Значение в максимальной точке для функции — самое большое значение функции на промежутке значений \[y_{\max }\]
Минимум точки у значения функции — это значение точки \[x_{0}\] для заданной функции вида:y=f(x), при условии что для всех значений x из ее области справедливо неравенство \[f\left(x_{0}\right) \leq f(x)\]
Минимум функции — это значение функции в точке, которая имеет минимальное значение на промежутке. Окрестность точки — это заданный интервал \[\left(x_{0}-\varepsilon ; x_{0}+\varepsilon\right)\], где \[\varepsilon\] — некоторое множество наименьших положительных чисел.
Точки экстремума — это точки минимальные и максимальные по значениям.
Экстремум функции— это некое значение функции, которое отвечает заданным точкам экстремума.
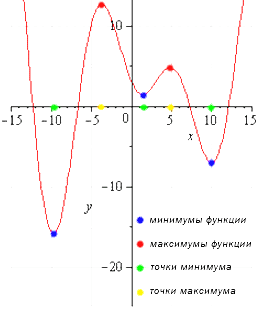
Следует помнить, что функциональный экстремум и его наибольшие, и наименьшие данные — это совершенно разные понятия.
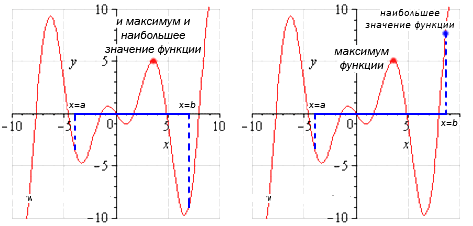
На первом графике максимальное значение функции на промежутке [a;b] будет достигаться в точке максимума и наибольшему по значению данному у функции. Второй график отражает следующее: значение функции в точке x=b, которая, в свою очередь не относится к точке максимума.
Условие достаточности для возрастания и убывания функции
Исходя из условия достаточных признаков увеличения и уменьшения функции определяются пределы возрастания и убывания функции.
Основные определения характеристик возрастания и убывания функции на заданном интервальном промежутке:
- когда значение производной функции, имеют следующий вид: y=f(x) является положительной для каждого значения x из заданного промежутка X, тогда значение функции будет возрастать на X;
- когда производная функции отрицательна y=f(x) при любом значении x из интервала значений X, следовательно, функция будет иметь убывающий вид.
Для того, чтобы определить промежутки, на которых будет возрастать и убывать функция, нужно выполнить следующие условия:
- определить значение производной для функции;
- найти значение неравенства \[f^{\prime}(x)>0 \text { и } f^{\prime}(x)<0\] на заданной области определения;
- к найденным значениям промежуток нужно прибавить точки, которые расположены в начале и в конце границы. И функция имеет положение определенной и непрерывной.
Пример №1:
Необходимо найти промежутки возрастания и убывания значения функции, используя алгоритм решения.
Задана функция: \[y=\frac{x^{3}+4}{x^{2}}\]
Определим область значения данной функции.
Для нашего примера, обязательно условие: знаменатель не должен равняться нулю. Поэтому \[D(y): \quad x \in(-\infty ; 0) \cup(0 ;+\infty)\]
Определяем значение производной функции:
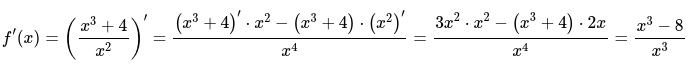
Вычисляем необходимые промежутки, где функция возрастает и убывает функции по признаку достаточности и решаем следующее неравенство: \[\frac{x^{3}-8}{x^{3}}>0 \text { и } \frac{x^{3}-8}{x^{3}}<0\] на области определения.
Для решения нужно воспользоваться методом интервалов. Единственным подкоренным значение для числителя является значение x = 2. При этом знаменатель преобразуется в нулевое значение и x=0.Данные точки делит область определения на промежутки, в которых значение производной функции сохраняет свой первоначальный знак.
Все точки на числовой прямой отмечаются. Плюс и минус — это интервал, где производная имеет положительное значение и отрицательное соответственно.
Нижние стрелки отражают возрастание или убывание функции на заданном соответствующем интервале значений.
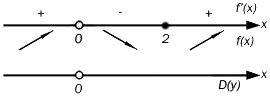
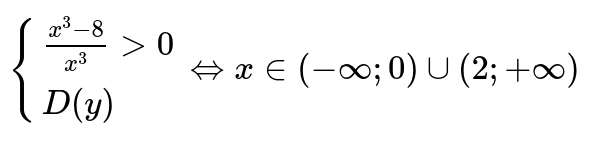
Следовательно:
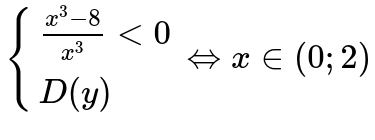
В определенной точке равной x=2 функция определена и является непрерывной. Ее следует отнести к промежутку, где функция возрастает и убывает.
В точке со значением x=0 функция не определена. Поэтому ее нужно полностью исключить из промежутка.
Изобразим график функции для отражения полученных в процессе вычислений значений.
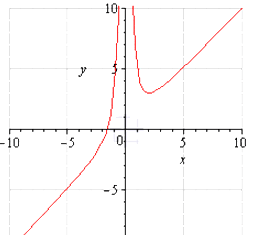
Ответ: Заданная функция будет возрастать при следующих значениях \[x \in(-\infty ; 0) \cup[2 ;+\infty)\] и убывать на интервале (0;2].

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Достаточные условия для определения экстремума функции
Для определения максимальных и минимальных значений функции используется любой из трех признаков экстремума. Функция обязательно должна удовлетворять их требованиям. Самым распространенным и простым является первый способ.
Первое условие экстремума выполняется следующим образом: при условии что заданная функции вида: y=f(x) имеет дифференцируемое значение в \[\varepsilon\] — крайние значения точки \[x_{0}\], а главной точке \[x_{0}\] имеет непрерывное значение. Следовательно:
- если \[f^{\prime}(x)>0\] при значениях \[x \in\left(x_{0}-\varepsilon ; x_{0}\right) \text { и } f^{\prime}(x)<0 \quad x \in\left(x_{0} ; x_{0}+\varepsilon\right)\], тогда \[x_{0}\] — максимальное значение точки;
- если \[f^{\prime}(x)<0 \text { при } x \in\left(x_{0}-\varepsilon ; x_{0}\right) \text { и } f^{\prime}(x)>0 \text { и } x \in\left(x_{0} ; x_{0}+\varepsilon\right)\], тогда \[x_{0}\] — минимальное значение.
Иными словами:
- в случае, если \[x_{0}\] функция непрерывная и в ней производное значение изменяется с плюса на знак минус, из этого следует, что \[x_{0}\] — точка максимума;
- если в точке \[x_{0}\] значение функции непрерывное и для нее производная меняет знак с минуса на плюс, \[x_{0}\] — минимальная точка.
Алгоритм определения неизвестных точек экстремума по первому признаку
- Нужно определить область определения функции;
- Вычислить производную для функции на заданной области определения;
- Вычисляются нулевые значения в числителе и нулевые данные в знаменателе производной. Нужно найти неизвестные точки области определения, где производная уже не существует;
- Данные точки разделяют область определения функции на конкретные отрезки и промежутки, в которых значение производной сохраняет свой первоначальный знак.
- Находим характер знаков для производных значений на каждом конкретном из интервалов;
- Нужно выбрать точки, в которых функция будет являться непрерывной и, проходя через значения, где производная меняет свой знак. Следовательно, данные точки будут относиться к точкам экстремума.
Пример №2:
Нужно используя алгоритм решения определить экстремумы функции: \[y=\frac{2(x+1)^{2}}{x-2}\]
Так как область функции всех значений считается множество натуральных простых чисел, за исключением значения x=2.
Определяем значение производной:
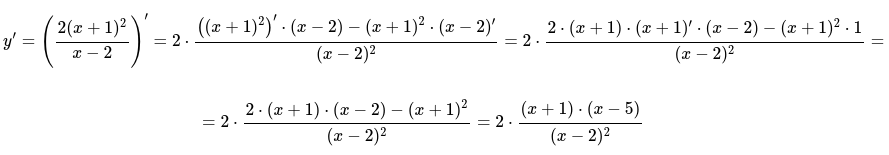
Нулевыми значениями числителя значатся точки равные x=-1 и x=5, знаменатель преобразует свое значение в ноль при x=2. На числовой оси нужно отразить все имеющиеся точки значений:
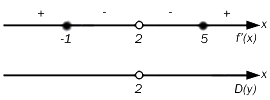
Находим значения знаков производной на каждом конкретном интервале значений.
Для этого необходимо вычислить значение производных значений в каждой из точек заданного промежутка (интервала).
Например, в точках x=-2, x=0, x=3 и x=6.
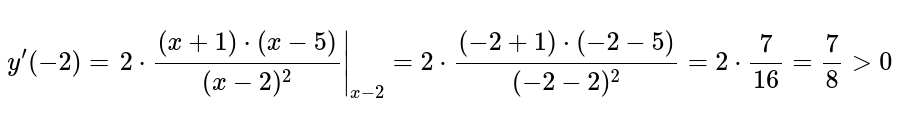
Следовательно, на заданном интервале \[(-\infty ;-1)\] производная функции имеет положительное значение (на графике нужно обозначить знак плюс над интервалом).
Аналогичным образом определяются и другие значения производной:
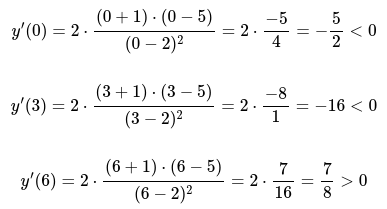
Выполнив все решения, над вторым интервалом нужно поставить знак минус, а над третьим также минус. Для четверного интеграла будет соответствовать плюсовое значение.
Далее нужно выбрать точки, при которых функция будет иметь непрерывный вид, а ее производная изменит свой первоначальный знак. Определенная в ходе вычислений точка будет значится как точка экстремума.
Для значения точки x=-1 функция является непрерывной и ее изменяет свой знак с положительного на отрицательный.
Следовательно, исходя из первого признака экстремума, x=-1 – максимальная точка и ей соответствуем максимум значения функции.
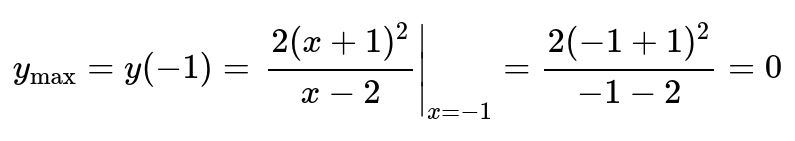
При значении x=5 функция является непрерывной и производное значение будет изменять знак с положительного на отрицательный.
Поэтому, x=-1 – точка с минимальным значением, и ей будет относиться минимум функции.
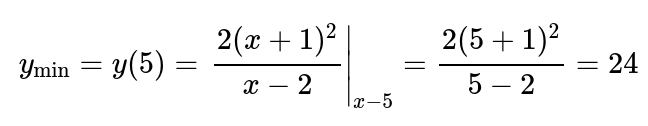
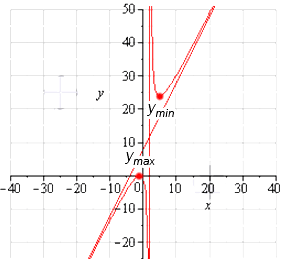
Открытый интервал и определение неизвестных максимальных и минимальных точек функции
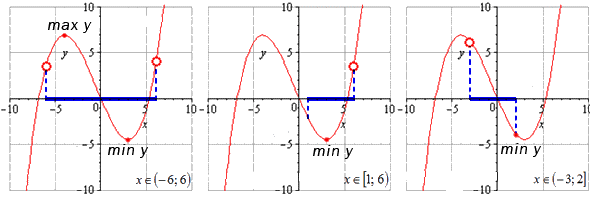
Рассмотрим первый график на вышеуказанном рисунке и увидим, что обозначенная на нем функция принимает максимальное и минимальное значение в точках на открытом интервале, который равен (-6;6).
Если задать интервал значений, который равняется (1;6), то увидим, что минимальное числовое значение функции будет достигнуто в точке стационара. Наибольшее выражение, мы определить не можем, оно нам остается неизвестным. В случае, если бы значение x принадлежало бы интервалу 6, то оно бы было равным данному числу.
Подобный случай изображен на соседнем графике. На нем наименьшее значение функция будет иметь в правой границе. Которой характерен интервал значений (-3;2). Что касаемо максимального значения, точного вывода в данной ситуации сделать невозможно.
Наибольшее и наименьшее значение функции на отрезке
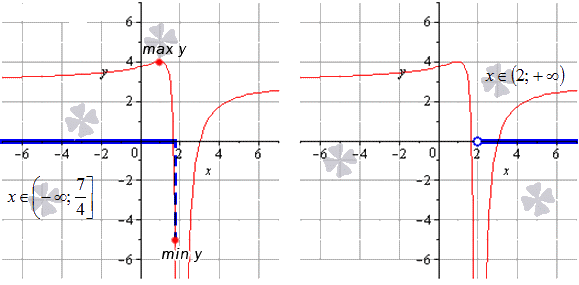
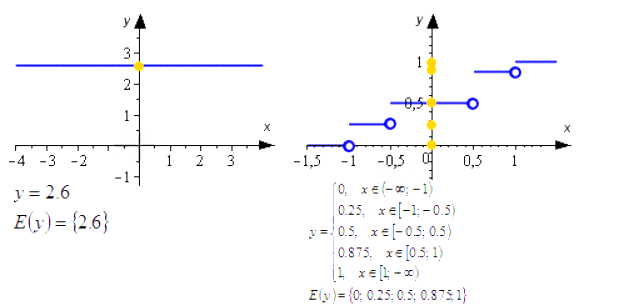
На данных графиках, мы можем увидеть, что максимальное числовое значение в точках, имеющих абсциссу равную значению один. Она достигает минимального значения также с правой стороны на границе интервалов. На значении минус бесконечность, рассматриваемая функция будет приближаться к конкретным точкам y=3.
Рассмотрим для примера интервал значений x ∈ ( 2 ; + ∞ ) x∈2; +∞. Проанализировав все характеристики функции, можно сказать следующее: ни минимального ни максимального значения функция на данном промежутке не примет. Когда x будет стремиться к значению два, то сама заданная функция, соответственно будет приближаться к значению минус бесконечность.
Если абсцисса приближается к значению +∞, то функция будет приближаться к значению 3.
Принцип определения наибольших и наименьших значений функции на отрезках
Рассмотрим последовательность проведения основных операций, для определения нужных нам числовых значений для определенной функции:
- Для начала задается область определения функции. Далее необходимо провести ее анализ и проверить входит ли в ее пределы заданный отрезок.
- Определяем точки, на отрезках, в которых не существует первой точки. Это показательно, для функций у которых аргумент обозначается в виде модуля. А также, данную характеристику можно встретить у степенных функций, у которых показатель — простое рациональное числовое значение.
- Вычисляем определение производной функции и приравниваем ее к нулевому значению. Составляем нужное нам уравнение и подбираем корневые значения. Если ни одна стационарная точка не попадает в заданный нами отрезок, нужно применить другие действия. Расписанные в пунктах 4 и 5.
- Вычисляем значения в стационарных точках, если они не существуют в первой производной
- В конечном итоге мы получаем ряд числовых значений. Далее начинаем выбирать самое максимальное и минимальное значение, для функции, которые мы хотим определить.
Весь приведенный алгоритм решения, рассмотрим на конкретном примере, для лучшего восприятия информации.
Задано условие задачи:
Функция следующего вида \[y=\frac{x^{3}+4}{x^{2}}\]
Необходимо определить значения, которые будут отражать максимальное и минимальное числовое значение на заданном отрезке. Отрезок отображает следующие значения [1;4]]-4;1].
Выполняем все необходимые действия, применяя наш уже изученный алгоритм решения.
Определяем область функции, которая равняется действительным числам, отличным от нулевого значения.
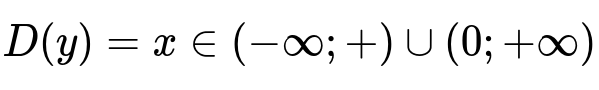
Два отрезка, определенно, будут находится в области определения. Затем по известным формулам, определяем производное значение функции.
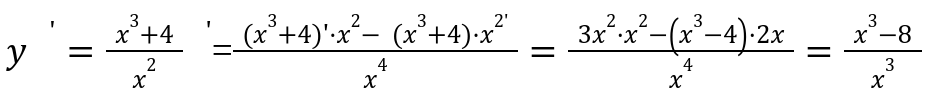
Из уравнения мы определили, что производная значения функции, будет существовать во всех точках заданных отрезках.
Далее, при помощи определенного нами уравнения, вычислим значения стационарных точек.
\[\frac{x^{3}-8}{x^{3}}=0\]
Уравнение имеет только один корень действительного числа, он равняется значению два. Это и будет стационарная точка, которая будет попадать в отрезок [1;4]
Определяем значения на концах отрезка, в данной точке.
А именно: x=1, x=2, x=4.
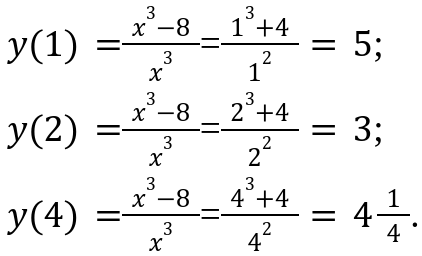
Мы определили максимальное значение, которое можно записать в следующем виде max y=y(2)=3. Данная запись будет актуальна, при x=1, минимальное значение min y=y(2)=3 — когда х=2.
Что касаемо второго отрезка, то ни одно стационарной точки, он в себя не включает. Поэтому вычисляем значения на концах заданного отрезка.
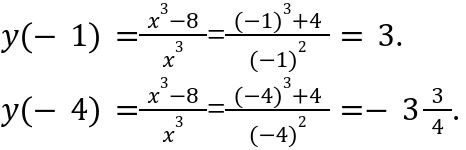
Следовательно: максимальное значение будет равняться трем, а минимальное будет равно — \[-3 \frac{3}{4}\].
Максимальные и минимальные значения функций на открытом и бесконечном значении интервала
Перед тем как начать разбирать новый способ, нужно вспомнить и повторить, как правильно определяются пределы односторонних значений и пределы значений бесконечности. А также вспомнить главные методы их вычисления.
- Провести проверку, чтобы заданный интервал значений подходил под необходимую область значения функции;
- Определиться со всеми нужными точками, которые находятся в заданном интервале. И где отсутствует первая производная значения. Обычно это у функций, где аргумент является в знаке модуля. Функции со степенью, с дробно рациональным показателем.
- Затем будем определять, постоянные точки, относящиеся в конкретный заданный промежуток. Значение производной, нужно приравнять к 0. Для этого решаем уравнение и подбираем необходимые корни значений. Если отсутствует стационарная точка или она не подходит под заданный интервал, значит переходим к следующему шагу. Его характеризует интервальный вид. Когда интервал выглядит как: [a;b), нужно определить правильные данные для функции в x = a и предел равный \[\lim _{x \rightarrow b-0} f(x)\];
Когда интервал задается как значения (a;b], то нам надо вычислить значение функции в точке x = b и односторонний предел \[\lim _{x \rightarrow a-0} f(x)\].
Заданный интервал ( a ; b ), нужно вычислить пределы \[\lim _{x \rightarrow b-0} f(x)\] и \[\lim _{x \rightarrow a+0} f(x)\];
Если задан промежуток: [ a ; + ∞ ), определяется необходимое значение в точке x = a и предел на плюс бесконечности \[\lim _{x \rightarrow+\infty} f(x)\];
Когда значение интеграла задается как промежуток: (-∞; b], вычисляем значение в точке x = b и предел на минус бесконечности \[\lim _{x \rightarrow-\infty} f(x)\];
Если ( − ∞ ; b ), то считаем односторонний предел \[\lim _{x \rightarrow b-0} f(x)\] и предел на минус бесконечности \[\lim _{x \rightarrow b-\infty} f(x)\];
Если же ( − ∞ ; + ∞ ), то считаем пределы на минус и плюс бесконечности \[\lim _{x \rightarrow b+\infty} f(x)\], \[\lim _{x \rightarrow b-\infty} f(x)\].
- В заключении необходимо сделать вывод на основании расчета по вычислению необходимых значений и промежутков функции. Это подразумевает несколько вариантов. Когда предел с одной стороной равен отрицательной бесконечности или плюс бесконечности. Становится очевидно, что о минимальном и максимальном значении функции ничего конкретного сказать нельзя. При его решении мы будем руководствоваться алгоритмом решения, приведённым выше по тексту.
По заданию нам дана задача, в которой указана функция.
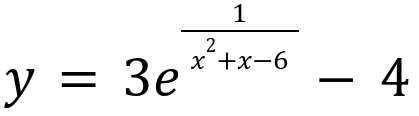
По условию необходимо определить минимальные и максимальные значения в интервалах. А именно: ( − ∞;-4), (-∞; -3), (-3; 1], (-3; 2), [1;2), (2; +∞); [4;+∞).
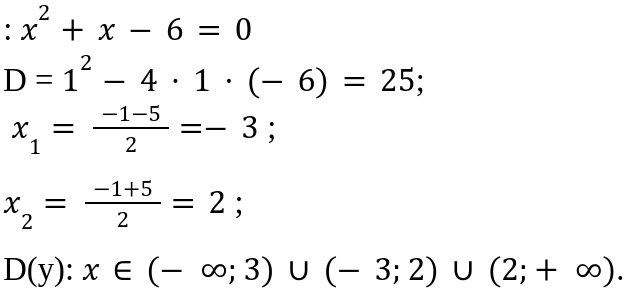
Затем выполним дифференцированный расчет функции и вычислим следующие данные:
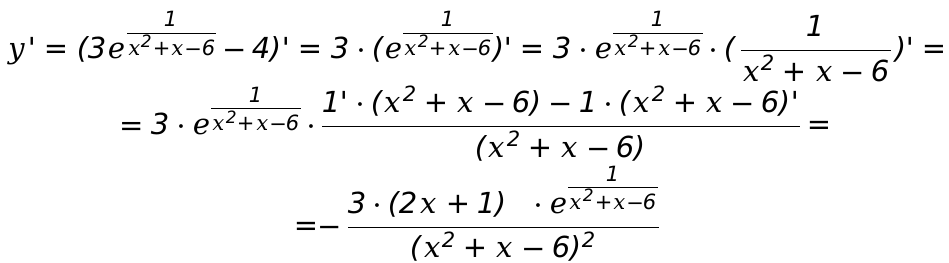
Следовательно, производные могут существовать на всей области. Определим значения стационарных значений точек. Производная функции равняется 0 при x = \[-\frac{1}{2}\]. Это точка, принадлежит интервалу значений ( − 3 ; 1 ] и (-3;2).
Подставим в функцию и вычислим значение при x = − 4 для заданного промежутка ( − ∞ ; − 4 ].
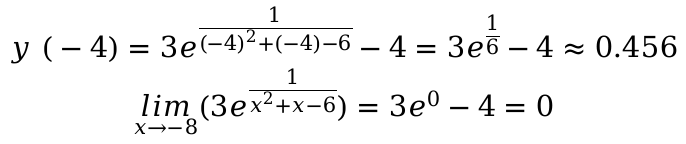
Так как \[3 e^{\frac{1}{6}}-4>-1\], максимальное значение \[\lim _{x \rightarrow(-\infty-4)}=y(-4)=3 e^{\frac{1}{6}}-4\]
Данная ситуация не дает возможности вычислить самое минимальное значение. Есть возможность, только сделать вывод, что в нижней части функции есть ограничение до -1. Так как к этому значению функция непосредственно приближается постоянно на значение бесконечности с отрицательным показателем. Признак второго интервала, там отсутствуют стационарные точки и границы предела. Поэтому выполнить вычисление максимум и минимум точек не представляется возможным.
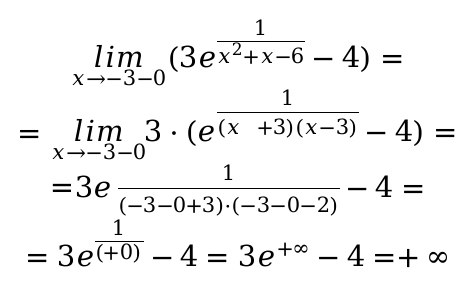
Чтобы подсчитать максимальное числовое значение заданной функции для третьего промежутка. Нужно вычислить ее значения в точке x = − 1 /2, при заданном значении x = 1. Также определяем односторонний предел в конкретной ситуации для точки, когда аргумент функции имеет стремление к − 3 с положительной стороны по значению:
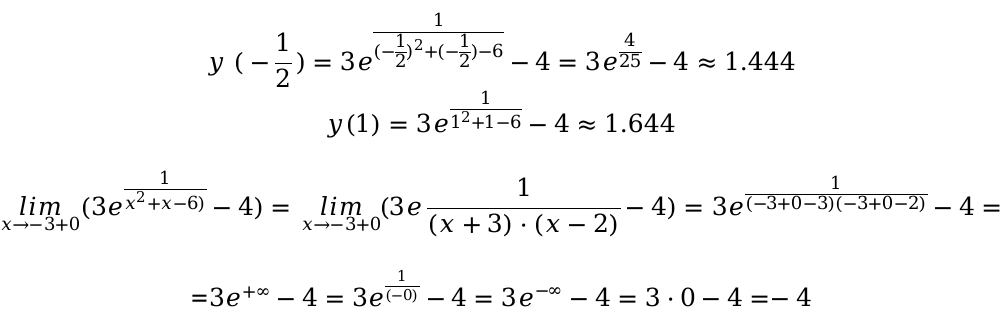
Следовательно \[y\left(-\frac{1}{2}\right)=3 e^{-\frac{4}{25}}\], а минимальное значение вычислить нет возможности. Функция ограничена снизу числовым значение равным (− 4). Следовательно, значения, которые у нас получились в предыдущих расчетах, на промежутке значений [ 1 ; 2 ) максимальное значение, функция будет принимать при x = 1. Вычислить наименьшее значение по математическим законам не возможно. На промежутке ( 2 ; + ∞ ) функция не может достигнуть максимального, а также и минимального значения. Так как функция принимает данные из интервала ( − 1 ; + ∞ ).