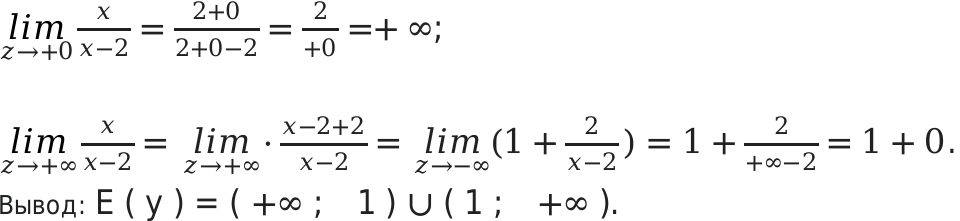Как найти область определения функции
Область определения функции: понятие
Функция задается тогда, когда любому значению, например x соответствует любое значение y. Независимой переменной называют значение х или по другому — аргументом. Числовое значение y, как правило, является зависимой переменной.
Данная зависимость между x и y в алгебре называют функциональной. Записывают ее в виде функции y = f(x)
Другими словами, функция, это когда значения одной переменной зависят от значений другой переменной.
Далее можно сформулировать определение область функции. То есть, на какой промежуток действе функции распространяется.
В математике под областью определения функции понимают множество, которое включает в себя все значения аргумента. Если функция имеет предел, то он является значением аргумента при котором функция возрастает или убывает. Область определения функции также называется областью допустимых значений функции.
Область функции можно выразить геометрически. Например, в виде графика. Где за основу берутся оси х и y.
Ограничение области определения
Область ограничения действительных чисел может быть от \[(0 ;+\infty)\].
Например: [-4;1)U[5,7).
Область определения может указывать на следующие характеристики:
- деление функции как \[y=x+\frac{2 \cdot x}{x^{4}-1}\];
- корень четной степени и переменная под корнем:
\[=\sqrt{x+1} \text { или } y=\sqrt[n]{2^{2 \cdot x+1}}\]
- переменная в основании степенного значения
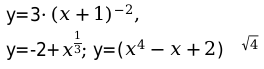
- логарифмическая переменная \[y=\ln \frac{x^{4}+x}{8} ; y=2+\]. Значения основания должно быть положительным. Также, как и логарифмическое значение.
- переменная тангенса и котангенса в виде следующего уравнения: y=arcsin (x+4)+4*x2.
Если отсутствует хотя бы один из перечисленных характеристик область определения функции определяется иначе.
Пример 1: \[y=\frac{x^{4}+2 x-x+2}{4}+2 \frac{2}{3} \cdot x\], в данном множестве нет переменной, поэтому и решается оно иначе.
Пример 2: \[y=\frac{3}{x-1}\], нужно вычислить область определения. Обязательно, при решении нужно уделить внимание на знаменатель. Потому что, по законам алгебры деление на ноль запрещено.
Получаем следующее действие:\[\frac{3}{x-1}\].
Область значения не должна быть равной единице, так как в знаменателе получим нулевое значение. Отсюда область определения будет в пределах \[(-\infty, 1) \cup(1,+\infty)\].
Область определения для суммы, разности и произведений числовых значений
Чтобы правильно уметь определять данную область, нужно знать следующие утверждения: если функция вычисляется, при помощи суммы: \[f_{1}+f_{2}+\ldots f_{n} \text { или } \mathrm{y}=f_{1}+f_{2}+\ldots f_{n}\]
Область определения будет следующего вида: \[\mathrm{D}(\mathrm{f})=\mathrm{D}\left(f_{1}\right)\left(f_{2}\right) \ldots\left(f_{n}\right)\]
Пример суммы числовых значений: возьмем уравнение: \[y=x^{7}+x+5+t g x\].
Решение: уравнение представлено в виде суммы нескольких значений, где степень равна семи, показатель один.
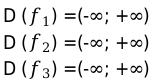
Области определения tg характерны все действительные числа.
Ответ: для заданной функции относится пересечение областей или количество действительных чисел кроме \[\pi / 2+\pi \cdot n \cdot n \in z\]
Пример разности значений:
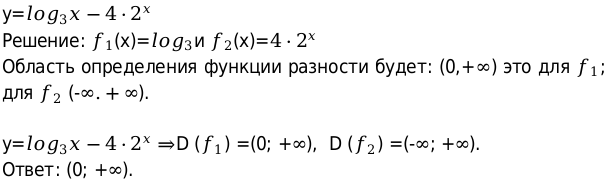
Пример произведения чисел:

Сложные функции х и y и их область определения и значения
Сложная функция имеет следующий вид: \[\mathrm{y}=f_{1}\left(f_{2}(\mathrm{k})\right)\]
D (f) — множество значений;
Пересечение двух множеств и будет являться областью определения функции сложного типа.
Примеры:
Представим функцию в виде: \[\mathrm{y}=f_{1}\left(f_{2}(\mathrm{k})\right)\]
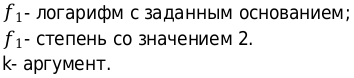
Используем изученные в данном уроке области определения:
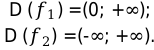
Исходя из этого получаем систему неравенства:
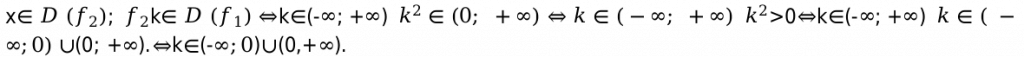
Ответ: все действительные числа, кроме нуля.
Область определения функции в виде дробного значения
Когда функция задается выражение в виде дроби. Переменная значений находится в знаменателе. Следовательно, область определения являются действительные числа. Исключением служит число, которое приведет знаменатель к нулевому значению.
Пример №1: \[y=\frac{x-4}{x+4}\]. Решив уравнение, определим искомое значение области определения. Которое является \[-\infty ;-4 \cup-4 ;+\infty\]
Пример №2: \[y=\frac{1}{x^{2-1}}\];
Искомая область: \[-]-\infty ;-1[\cup]-1 ; 1[\cup] 1 ;+\infty[.\]
Пример №3. \[y=\cos x+\frac{3}{x^{2}-4}\].
Первое слагаемое имеет область определения множество действительных чисел. Второе — также все числа, кроме -2 и 2, они приведут знаменатель к нулю. Область определения должна соответствовать условиям двух слагаемых и равняться действительным числам, кроме -2 и 2.
Область определения тригонометрических функций
Множество значений всех действительных чисел, будет являться областью определения функций синус и косинус, и записываться следующим образом.
Функции являются ограниченными, как сверху, так и снизу, y = sin x и y = cos x. Промежуток их действия сводится к неравенству -1 ≤ y ≤ 1
Областью определения функции тангенс tg x, является выражение \[\mathrm{x} \neq \frac{\pi}{2}+\pi k, \mathrm{k} \in z\].
Областью определения функции y = ctg x является множество чисел \[x \neq \frac{\pi}{2}, \quad k \in z\].
На нижеприведенных примерах подробно расписано решение задач, при определении области функции, при заданных промежутках значений.
Пример №1
Определить область значения функции sin x
Данный вид функции относится к категории периодической. Ее период равняется 2п.
Определяем множество значений на следующем отрезке:( 0;2).
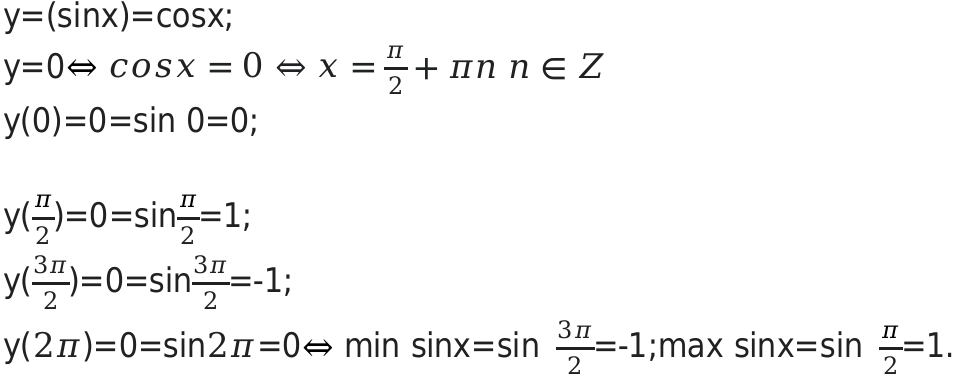
Пример №2:
Необходимо определить область значения функции cos x.
Наименьшее значение равно -1;
Минимальное значение косинуса равняется -1, потому что наименьшее значение х, на окружности стремится к этому значению и следовательно равняется -1.
Максимальное значение косинуса будет соответственно 1. Поскольку значение на окружности х имеет число 1.
Область значение, следовательно, будет от минус одно до плюс одного. [-1;1].
Применяем двойное неравенство и записывает следующее выражение:
\[-1 \leq \cos x \leq 1\]
Область значения косинуса никогда не зависит от аргумента, только если сам аргумент выражен в виде сложного выражения. Где имеют место ограничения касающиеся области определения и области значения.
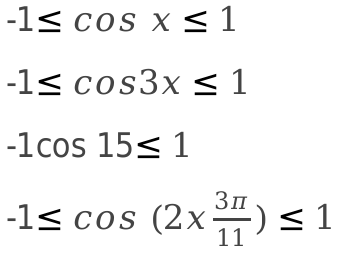
Таким образом, минимальное значение cos x, cos (15a), cos(5-11x) и так далее, будет однозначно равняться -1;
Самым максимальным значением cos x, cos(4φ), cos(5х+3) равняется 1.
Область значений функции y=cos x — также промежуток [-1;1].
Область значения квадрата косинуса, будет промежуток от нуля до единицы[0;1]. Потому что число в четной степени, является не отрицательным.
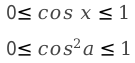
Аналогичным образом находим область значений модуля косинуса — промежуток [0;1]
Пример №3
y = tgx на определенном интервале \[\left(-\frac{\pi}{2} ; \frac{\pi}{2}\right)\]
Решение:
Из правил алгебры, известно, что производная тангенса имеет положительное значение. Соответственно функция будет иметь возрастающую характеристику.
Далее необходимо определить поведение функции, в заданных пределах.
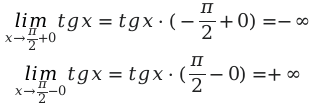
Выполнив решение, мы получаем рост значений от минус до плюс бесконечности. Решение будет сводиться к следующему: множество решение заданной функции, будет множество всех действий функции.
Пример №4
\[y=(\arcsin x)=\frac{1}{\sqrt{1-x^{2}}}\] на определенном интервале (-1;1).
Решение:
Для всех значений x производная будет положительной, в пределах от -1;1
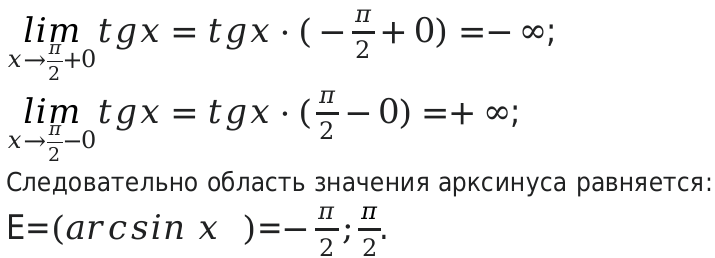

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Область определения показательной и логарифмической функции
Показательная функция записывается как: y = kx, где значения:
- x — показатель степени;
- k — число, которое обязательно больше нуля и не равно единице.
Область определения показательной функции — это множество значений R.
Основные примеры показательных функций:
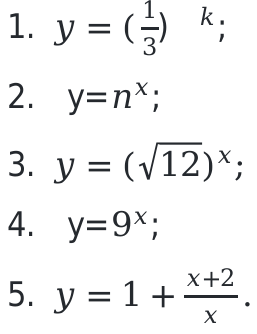
Область определения, для этих функций, записывается следующим образом: \[(-\infty,+\infty)\].
Логарифмическая функция выражается как: y=log nk
Где значение n, имеет значение больше нуля и не менее единицы.
Область определения логарифма и логарифмической функции — это множество положительных значений и действительных чисел.
Рассмотрим на примере, характер решения задачи данной функции.
Пример №1:
y = lnx , определить область определения натурального логарифма.
На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.
Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.
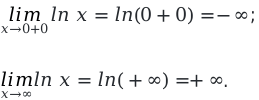
Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.
Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.
Ответ: множество всех действительных чисел, это и есть область значений функции ln.
Определения области значения функции x
На примерах рассмотрим, как определить области значений функции.
Первоначально, необходимо определить значения непрерывной функции y=f(x).
Известно, что функция непрерывная и достигает своих максимальных max f(x) и минимальных min f(x) значений, на разных периодах. Из этого следует отрезок, где находятся значения исходной функции. Тогда решение состоит в нахождении точек максимума и минимума.
Пример №1 :
Необходимо вычислить область значений уравнения y = x4 — 5x3 + 6x2 на отрезке [ 1 ; 4 ] [1; 4].
Для решения задачи необходимо произвести следующие действия:
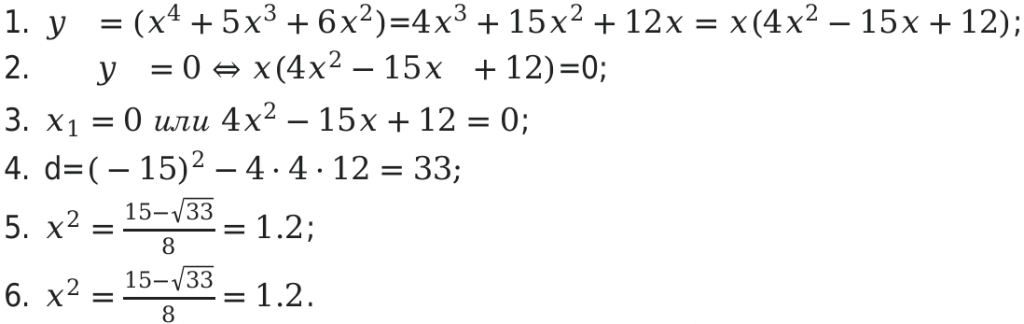
Следующим шагом будет определение значений функции в конечной и начальной точках.
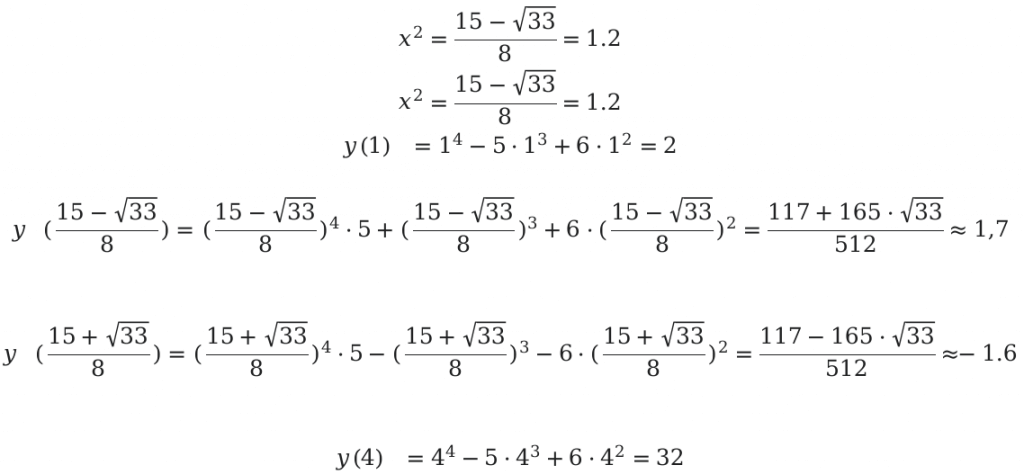
Ответ: \[\left(\frac{117-165 \cdot \sqrt{33}}{512} ; 32\right)\]
Пример №2.
Необходимо вычислить область значений уравнения
y = x4 — 7x3 + 5x2 на отрезке [ 1 ; 4 ] [1; 4].
Для решения задачи необходимо произвести следующие действия:
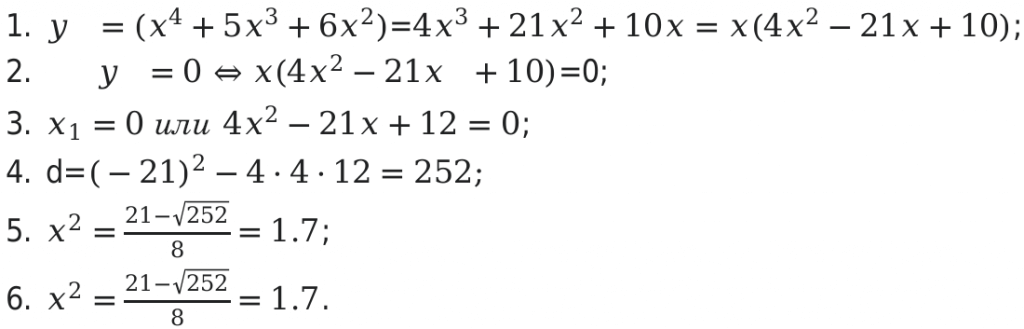
Следующим шагом будет определение значений функции в конечной и начальной точках.
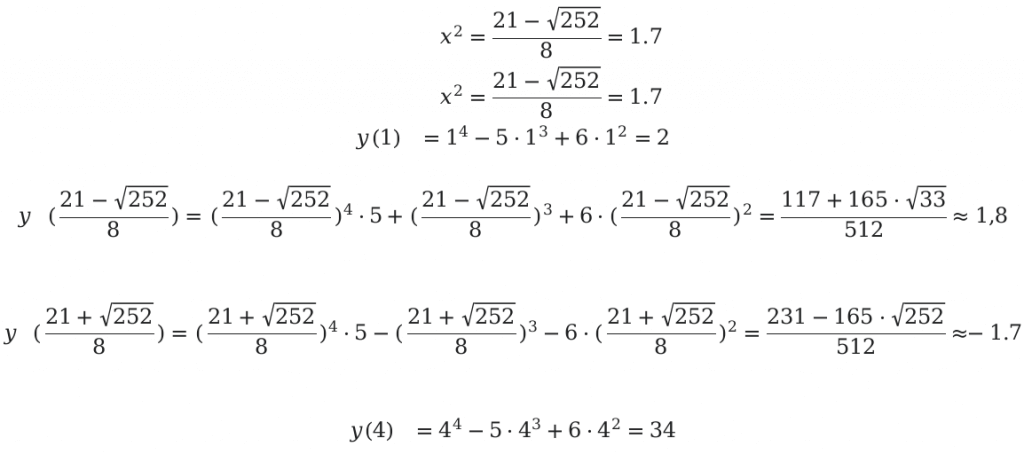
Ответ: \[\left(\frac{231-165 \cdot \sqrt{33}}{512} ; 34\right)\]
Пример №3 :
На этом примере подробно рассмотрим, как вычисляются значения непрерывной функции y= f(x), в определенных промежутках.
Для этого, первоначально вычислим:
- наименьшее и наибольшее значение;
- определим промежуток возрастания и убывания функции;
- односторонние пределы;
- предел бесконечности.
Решение:
Для решения возьмем функцию \[y=\frac{1}{x^{2}-4}\] и вычислим область значений на промежутке (-2;2).
Находим наименьшее и наибольшее значение функции на заданном отрезке.
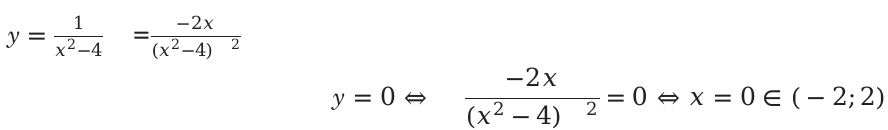
Из данных вычислений видно, что максимальное значение равно 0, так как в этой точке происходит перемена знака функции и соответственно функция начинает убывать.
А именно: \[y(0)=\frac{1}{0^{2}-4}=-\frac{1}{4}\]
\[-\frac{1}{4}\] — будет являться наибольшим значение заданной функции.
Следующим шагом в нашем решении, будет выяснение направления функции. Когда x значение стремится к (-2) и (+2).
В алгебре иными словами эти значения называют односторонними пределами.
Решение выглядит следующим образом.
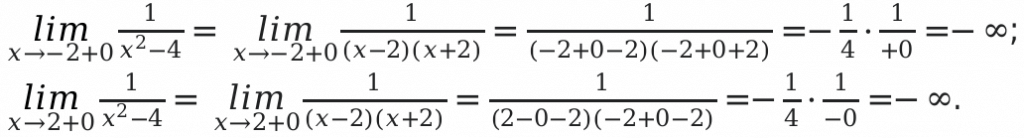
В конечном итоге мы получаем, что в пределах от -2 до 0, функции будут возрастать \[\text { От }-\infty \text { до }-\frac{1}{4} \text {. }\]
Если аргумент меняется, от 0 до то наоборот будет убывать к \[-\infty\].
Следовательно, необходимое множество значений будет на интервале \[-\infty \text { до }-\frac{1}{4}\].
Ответ: \[\left(-\infty-\frac{1}{4}\right)\]
Область определения функции y
Пример №1:
Данная функция имеет определенное значение, только при положительных значениях. \[D(y)=(0 ;+\infty)\].
Производная будет иметь следующий вид: \[y=(\ln x)=\frac{1}{x}\].
Так как функция имеет положительное значение, то на всем промежутке будет наблюдаться ее возрастание. От \[-\infty \text { до + — }\].
Поэтому область значения — это множество всех натуральных значений.
Пример №2:
У функции \[y=\frac{9}{z^{2}-1}\];
Если значение z имеет положительное значение, то функция будет считаться определенной.
Вычислим наибольшее и наименьшее значение, а также промежутки возрастания и убывания.
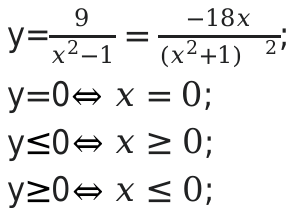
Если значение x будет больше, либо равным 0,то функция будет убывать.
Если значение x будет меньше либо равным нулю , функция будет возрастать.
Затем рассмотрим поведение функции и ее значения на бесконечной прямой.
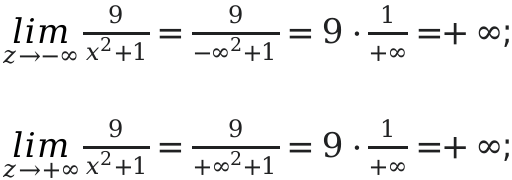
Вывод: если аргумент изменяется от \[-\infty\] до 0, тогда значение функции увеличиваются от 0 до 9 . Когда значения аргумента меняются от 0 до \[+\infty\], значения функции будут уменьшаться от 9 до 0.
Пример №3:
Определить область значений \[y=\frac{x}{x-2}\];
По правилам математики, знаменатель не может равняться нулю. Поэтому: \[D(y)=(-\infty ; 2)(+\infty ; 2)\].
Определим множества на первом отрезке. \[(-\infty ; 2)\]. На этом отрезке функция будет убывающей и значение отрицательным:
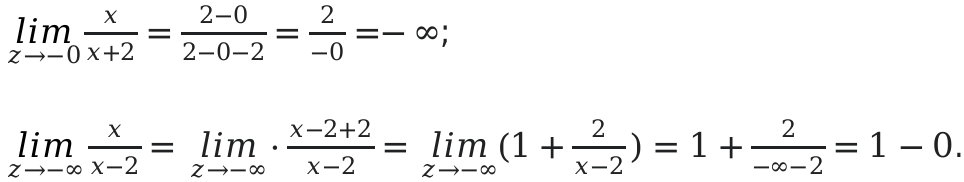
Функция ассиметрично начнет приближаться к 1, когда аргумент будет изменяться к минус бесконечности.
Определим множества на втором отрезке \[(+\infty ; 2)\].
На этом отрезке функция будет также убывающей: