Формула Эйлера для комплексных чисел
Свое название данная формула получила от имени известного ученого, математика Л. Эйлера. Именно этот ученый и является основоположником и в свое время ввел формулу в работу.
Формула Эйлера позволяет установить взаимосвязь между показательной функцией с тригонометрическими функциями.
Тождества и формулы Эйлера для комплексных чисел
Формуле Эйлера характерно следующее утверждение:
Для различных значений действительных и комплексных чисел x выполнено равенство:
\[e^{i x}=\cos x+i \cdot \sin x\]
где:
- e — экспонента значения;
- i — нейкая мнимая единица.
Значение экспоненты определяется по следующей формуле:
Для комплексного значения которое равняется: \[z=x+y i\] выполняется соответствующее условие:
Когда значение z является вещественным значение и равным \[I_{m z}=0\], равенство имеет следующий вид:
Когда числовое значение z представлено как мнимое: \[\left(R_{e z}=0\right)\] из этого следует следующее выражение:
Используя на практике формулу Эйлера получаем получается следующее выражение:
Комплектное значение z, выраженное как тригонометрическая формула (выражение):
где:
\[\mathrm{r}=|z|=\sqrt{x^{2}+y^{2}}\] значение модуля данного числа.
Используя формулу Эйлера, записывается следующее выражение:
Формула Эйлера позволяет определить неизвестные значения тригонометрических функций sin и cos, используя соответствующие формулы:
Понятие тригонометрической функции от некой комплексной переменной значения. Для значения x=iy выражают следующие формулы:
Тождество Эйлера, которое связывает между собой пять основных констант математики.
Данное выражение является частным случаем, когда значение x равняется переменной \[\pi\].
Применяя формулу Эйлера можно выразить следующие тригонометрические и показательные формы (виды), которые характеризуют действительные, комплексные числа.
Тригонометрическая форма записи некое представление комплексных значения в следующем виде: \[z=r \cdot(\cos \varphi+i \cdot \sin \varphi)\]
где:
r — значение модуля, заданного комплексного числового значения;
Данный модуль определяется по формуле:
\[\varphi\] −значение аргумента, который относится к комплексному числу z.
Значение аргумента вычисляется по формуле:
Комплексные числа, которые выражены в виде тригонометрических формул и форм
Применяя формулу, составляет следующее выражение:
Вычисленное значение по предыдущей формуле записывается в тригонометрическую формулу:
Показательная форма — это комплектное значение любого числа равное и выраженное в виде формулы: \[\mathrm{z}=\mathrm{r} \cdot e^{i \varphi}\]
где: r — значение модуля;
Данный модуль определяется по формуле:
\[\varphi\] значение аргумента, который относится к комплексному числу z.
Значение аргумента вычисляется по формуле:
Возведение комплексных чисел в степень с показателями произвольных значений:
Круги Эйлера и соответствующие формулы
Рассмотрим формулу Эйлера на примерах:
Для вышеперечисленных формул характерен также и геометрический смысл.
Его сущность состоит в следующем:
- если возвести в степень любое значение числа z, тогда его модуль (некоторое расстояние до центральной оси), также возводится в эту же степень n;
- аргумент значения (угол поворота в градусах относительно осевой линии), будет увеличиваться в n раз, то есть в значение равное значению возводимой степени.
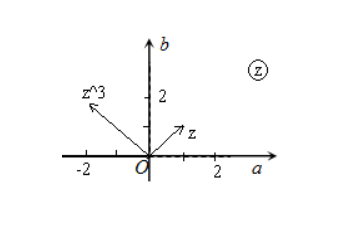
Формула, которая отражает возведение в степень, для конкретного комплексного числа, является верной не только для целых чисел n. Она также справедлива и для действительных чисел.
Следовательно, комплексная форма, которая выражения числа, позволяет определить корневое значение любой степени для произвольного ряда действительного числа.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры применения формулы Эйлера, для решения задач разного типа
Пример №1:
Необходимо представить все комплексные значения чисел в показательной форме.
- \[\mathrm{z}=2+0 i\]
- \[\mathrm{Z}=\frac{3}{2}+\frac{3}{2} \cdot i\]
- Чтобы представить значения в показательной форме, нужно записать ее основную формулу:
Из условия задачи следует, что a=2, b=0.
Определяется модуль начального (исходного) комплексного значения:
Затем определяется исходный аргумент, используя необходимую формулу:
Искомое представление значение комплексного числа \[\mathrm{z}=2 \cdot e^{i 0}\]
- Из условия задачи следует, что \[a=\frac{3}{2}, b=\frac{3}{2}\]
Используя нужные формулы можно вычислить модуль исходного значения комплексного числа:
Аргумент исходного значения для комплексного числа определяется по следующим правилам:
Все значения, которые определены в ходе решения, подставив в формулу и получим окончательный ответ задачи:
Из этого следует, что \[Z=\frac{3 \sqrt{2}}{2}\] является искомым значением представленного комплексного числа.
Пример №2:
Заданы значения комплексных чисел. Необходимо их представить в показательной форме, используя известные формулы и правила в ходе решения.
- \[\mathrm{z}=\sqrt{3}\]
- \[z=5 \cdot(\cos 2 \pi+i \cdot \sin 2 \pi)\]
Для определения данных задачи применим алгоритм решения.
Для показательной степени характерно решение по следующей формуле:
Для определения значения модуля и аргумента используем следующую формулу и подставив известные нам значения:
Показательный вид будет представлен следующим образом: \[z=\sqrt{3} e^{2 \pi i}\]
Определим значение модуля и аргумента для значений:
Для данных значение показательная форма будет представлены в виде следующих значений: \[z=5 \cdot e^{2 \pi i}\]
Ответ: \[z=\sqrt{3 e^{2 \pi i}} \text { и } z=5 \cdot e^{2 \pi i}\]















