Метод Крамера – теорема, примеры решений
Краткая биография Габриэля Крамера
Габриэль Крамер — (нем. Gabriel Cramer), Швейцария, 31 июля 1704 г. родился в семье врача. Он уже в детстве опередил своих сверстников в развитии интеллектуальной деятельности и проявил завидную способность в математике. В 18 лет успешно защитил дипломную работу. Через два года Крамер выдвинул свою кандидатуру на пост преподавателя в университете в Женеве.
Юноша привлек внимание магистрата, поэтому для него и еще одного кандидата на должность преподавателя был учрежден отдельный факультет математики, где Крамер затем работал в течение последующих нескольких лет.

Учёный очень много путешествовал в Европу, принимая опыт известных математиков того времени, как – Иоганна Бернулли и Эйлера в Базеле, Галлея и де Муавра в Лондоне, Мопертюи и Клеро в Париже и других. Всю жизнь поддерживал с ними тесный контакт.
В 1729 г. Крамер возвращается на должность преподавателя в Женеве. В этот период времени участвует в Парижском конкурсе и занимает заслуженное второе место. Используя свой исключительный талант пишет много статей по самым разным дисциплинам: геометрии, истории, математике, философии.
В 1730 г. он выпускает труд по астрономии.
В 1740 году Иоганн Бёрнулли поручил Крамеру опубликовать сборник его произведений. В 1742 г. Крамер подготовил и опубликовал сборник в 4 -х томах.
В 1744 г. выходит посмертная книга Якоба Бернули брата Иоанна Бернули и двухтомная переписка Лейбницы с Иоанном Бернули. Эти работы вызывали большой интерес ученых по всему миру.
Крамер — один из тех, кто изобрел линейную алгебру. Одна из его наиболее известных работ «Введение в анализ алгебраических кривых», опубликованная в 1750 г. на французском.

В ней Крамер создает систему уравнений по линейным уравнениям и алгоритм, который позже будет носить его имя, — метод Крамера. Габриэль умер во Франции 4 Января 1752 года.
Метод Крамера – теоремы замещения и аннулирования
Перед решением систем линейных уравнений методом Крамера необходимо изучить две важные закономерности. К ним относятся: теорема аннулирования; теорема замещения.
Теорема замещения. Складывая произведения алгебраического дополнения какого-то столбца, а также произвольные чисел b1, b2, b3, получается новый определитель, в котором значения заменяют соответствующие элементы первоначального определения, соответствующие данному алгебраическому дополнению.

Теорема аннулирования. В сумме произведения компонентов одного столбца или таблицы и алгоритмических дополнений соответствующих элементов другого столбца – будут равняться нулю.

Применение метода Крамера для решения систем линейных уравнений (СЛАУ)
Для поиска ответов по задачам для решения систем линейных уравнений актуальна эта методика. Метод Крамера позволяет находить решение системы с количеством строк равным количеству неизвестного. Так решаются квадратные уравнения. В процессе нужно вычислить матричные определители, в том числе основные, и дополнительные, полученные с помощью замены одного столбца основного определителя на столбец со свободными членами системы алгоритмов. На рисунке можно найти наглядное представление алгоритма.
Для этого необходимо применить метод Крамера СЛАУ:



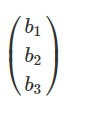
Рассмотрим решение системы уравнений методом Крамера:
Первое: вычислим определитель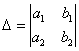 , а именно – определитель системы.
, а именно – определитель системы.
Если \[\Delta=0\] система имеет только 1 решение, чтобы найти корни, следует сделать вычислить еще два определителя:
На практике данные определители обычно могут быть обозначены обычной латинской буквой D. Чтобы найти корни уравнения используем следующую формулу:
Пример: Решите систему уравнений линейным методом Крамера
Решение: Из уравнения следует, что коэффициенты уравнения велики, в правой части уравнения видим десятичные дроби с запятой. Запятая – крайне редко можно увидеть в практике по математике, эта система взята из эконометрической задачи.
- Есть вариант выразить одну переменную через другую, это не самый удобный способ, так как мы получим дроби, с которыми невозможно будет работать, и будет хромать оформление самого решения.
- В таких случаях применимо правило Крамера.

Оба корня имеют бесконечные хвосты, решение дает лишь приближенное значение, что допустимо, если это задачи по эконометрике. Данное условие решается по готовым формулам, однако, есть одна деталь. Если используется данный метод, то обязательным условием, является использование вот этого фрагмента: 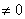 это значит, что уравнение имеет одно решение». Если этого не сделать, то при проверке вас могут наказать за пренебрежением теоремой Крамера.
это значит, что уравнение имеет одно решение». Если этого не сделать, то при проверке вас могут наказать за пренебрежением теоремой Крамера.
Оба корня имеют бесконечные хвосты, решение дает лишь приближенное значение, что допустимо, если это задачи по эконометрике. Данное условие решается по готовым формулам, однако, есть одна деталь. Если используется данный метод, то обязательным условием, является использование вот этого фрагмента: \[\neq 0\] это значит, что уравнение имеет одно решение». Если этого не сделать, то при проверке вас могут наказать за пренебрежением теоремой Крамера.
Важно сделать проверку, ее удобно провести на калькуляторе: подставляем приближенные значения \[a \approx-0,35 \quad b \approx 37,77\] в левую часть каждого уравнения системы. По итогу с небольшой погрешностью получаться числа, которые находятся в правых частях.
Метод Крамера — это простой метод решения линейных алгебраических уравнений. Этот вариант применим только к СЛАУ, в которых количество уравнений согласуется с неизвестным числом, а определитель не равен нулю.
Поэтому, когда вы изучили все шаги, вы можете продолжать использовать метод Крамера для решения алгоритма уравнения. Записываем их по порядку:
- Найти главный определитель матрицы:

Важно, чтобы определитель не имел значения – 0.
- Ищем определители:

В итоге получаем, определители матриц, которые мы вывели из матрицы A заменяя столбцы на свободные члены.
- Найдем неизвестные переменные значения:
Тут важно помнить тождества Крамера, при помощи которых, можно найти корни или по-другому неизвестные переменные.
- Выполняем проверку:
Мы проверяем решение, подставляя x, y и z в исходную СЛАУ. Все уравнения в абсолютной системе необходимо преобразовать в тождества. Вы также можете вычислить произведение матрицы A * X. Если результатом является матрица, равная B, система решена правильно. Если он не равен B, то одно из уравнений, вероятно, содержит ошибку.
Давайте сначала рассмотрим систему, состоящую из двух линейных уравнений, потому что она проще и поможет вам понять, как правильно использовать правило Крамера. Если вы разбираетесь в простых и коротких уравнениях, вы можете решать более сложные системы из трех уравнений с тремя неизвестными.
Среди прочего, существуют уравнения с двумя переменными, и решение этих уравнений целиком связано с правилом Крамера.
Пример. Таким образом, дана система, состоящая из двух линейных уравнений:
- Ищем главный определитель системы:
• Это означает, что если \[\Delta=0\], то либо у системы много решений, либо у системы нет решений. В этом случае нет смысла использовать правило Крамера, потому что решение не будет работать, и вам нужно запомнить метод Гаусса, который можно использовать для быстрого и простого решения этого примера.
Если \[\Delta \neq 0\], система имеет только одно решение, но для этого необходимо вычислить два других определителя и найти корень системы.
На практике определитель обычно может быть представлен не только \[\Delta\], но и латинской буквой D, что тоже правильно.
- Найти корни уравнения несложно, ведь главное знать формулу:
Теперь, когда мы можем решить двух линейные уравнения, мы можем решить трех линейные уравнения без каких-либо проблем. Для этого мы рассмотрим систему:
Здесь алгебраическим дополнением элементов является первый столбец \[A_{11}, A_{21}, A_{31}\]. При решении не забывайте и о других элементах. Следовательно, в системе линейных уравнений вам нужно найти три неизвестных — x, y, z и другие известные элементы.
Составим определитель системы из коэффициентов неизвестных: мы умножаем каждый член уравнения на \[A_{11}, A_{21}, A_{31}\] — алгебраическое дополнение элементов в первом столбце (коэффициент при x), а затем складываем все три уравнения вместе. У нас есть:
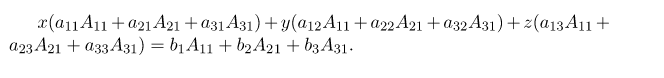
Согласно теореме о разложении коэффициент при x равен \[\Delta\].Коэффициенты при y и z будут равняться нулю по теореме аннулирования. Правая часть равенства по теореме замещения даёт новый определитель, который называется вспомогательным и обозначается:
Далее, можно записать равенство:
Для нахождения y и z перемножим каждое из уравнений изначальной системы в первом случае соответственно \[A_{12}, A_{22}, A_{32}\] во втором \[A_{13}, A_{23}, A_{33}\] и прибавим значение.
Итог преобразований:
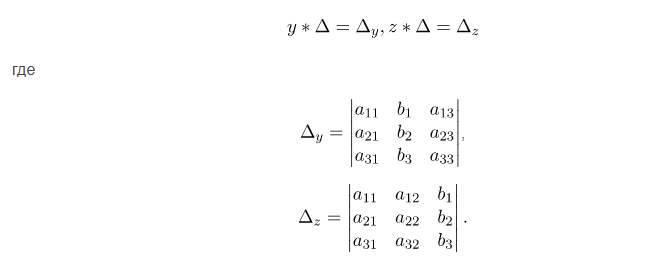


Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Алгоритм однородной системы уравнений: правила решения
Среди решений однородной системы могут быть, как нулевые решения (x = y = z = 0), так и решения отличны от нуля.
Линейная система является системой дифференциального уравнения.
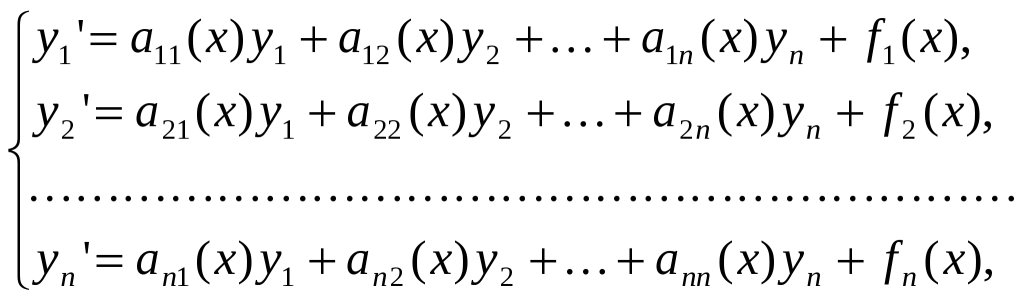
Где коэффициенты aij и fi – некоторые функции независимой переменной x. Будем считать их непрерывными; тогда для данной системы заведомо выполняются условия теоремы о существование и единственности решения задачи Коши. Если все fi=0, то система называется однородной, в противном случае она называется неоднородной.
При изучении линейных систем удобно использовать матричные обозначения.
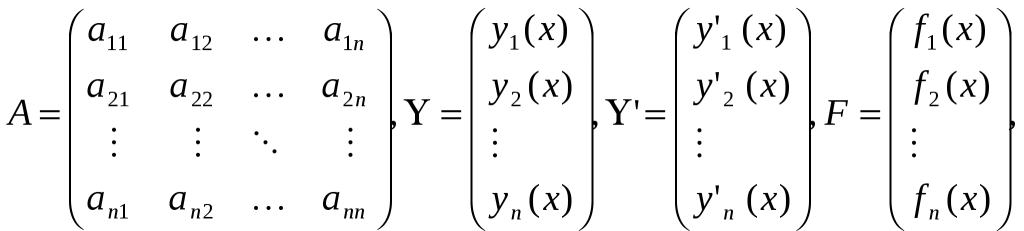
Позволяющие записать систему (1) в виде одного матричного уравнения
Так же, как и в случае линейных уравнений, общее решение неоднородной системы представляет собой сумму частного решения этой системы и общего решения соответствующей ей однородной системы. В свою очередь, общее решение однородной системы имеет вид:
Где С1,…,Сn— произвольные постоянные, а
Произвольные линейно независимые решения, называемые фундаментальным набором решений этой системы. Критерием линейной независимости этих решений является неравенство нулю определителя Вронского.
Решением системы линейных алгебраических уравнений называют набор значений неизвестных переменных \[x_{1}=\alpha_{1}, x_{2}=\alpha_{2}, \ldots, x_{n}=\alpha_{n}\] , обращающий все уравнения системы в тождества. Матричное уравнение \[A \cdot X=B\] при данных значениях неизвестных переменных также обращается в тождество \[A \cdot X=B\].
При помощи метода Крамера следует решать системы линейных алгебраических уравнений в том случае, если определитель не имеет значения 0. Использование этого метода поможет найти определители матриц такого порядка, как n на n. В случае, если свободные члены равны 0, тогда и их определители равны нулю, так как в них содержится столбец с нулевыми элементами. Поэтому, если определители имеют нулевое значение, лучше решать систему, используя метод Гаусса, а не Крамера, только в этом случае ответ решения будет правильный.