Множества чисел и примеры числовых множеств

Что такое множество чисел?

Математический термин «множество» можно охарактеризовать как отдельную совокупность, набор или объединение. Его элементами в теории могут быть различные объекты произвольной природы. К примеру, термин множество можно применить к большому количеству книг в библиотеке, товаров на полках магазина, студентов университета и т.д. В математике используются такие понятия, как множество точек отрезка заданной длины или множество парных чисел.

Для их математического обозначения используется определенный метод. В случае, когда какой-то элемент \[x\] принадлежит множеству A, тогда, тогда следует записывать \[x \in(A)\], если же ситуация обратная и элемент \[y\] не принадлежит множеству A, то правильно будет записать \[y \notin(A)\] или \[y \bar{\in}(A)\].

Если в множестве нет ни одного элемента, то его принято называть пустым множеством. Оно обозначается \[\phi\].

Для того, чтобы понять суть числовых множеств, рассмотрим несколько важных характеристик:

1. Два отдельных множества A и B будут называть равными и обозначаться A=B в том случае, если составляющие их элементы полностью идентичные.
2. Множество A будет называться подмножным множеством B в случае, когда каждый из элементов множества A является элементом второго множества B. В этой случае используются следующее обозначение \[A \subset(B)\]. Оно читается как A содержится в B, либо в B находится A.Очевидным является тот факт, что абсолютно в любое множество входит пустое множество \[\emptyset \subset A\]. Приведем пример. Если в состав множества A входят элементы 1, 2, 3, 4, 5, 6, 7, 8, 9, то оно записывается в виде: A={1, 2, 3, 4, 5, 6, 7, 8, 9}, а в B={2,3 ,5 ,7,9} тогда \[B \subset(A)\].
3. Объединением множеств называют случаи, когда множества элементов C, принадлежащих множеству A либо множеству B, или одновременно A и B. Обозначается объединение множеств следующим образом: \[C=\cup(B)\].
4. Пересечением множеств A и B в математике называют множества элементов C, принадлежащих сразу двум множествам A и B. Обозначается пересечение так: \[C=A \cap(B)\].

В случае, если A и B — это два множества точек, которые принадлежат двум геометрическим фигурам соответственно, тогда варианты их объединения будут выглядеть следующим образом:

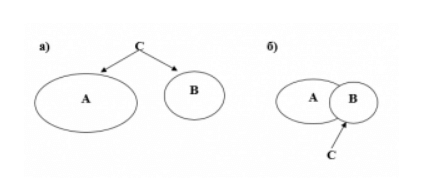
Если произойдет пересечение множеств A и B, то выглядеть это будет так:

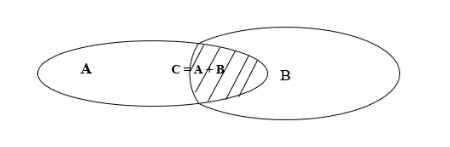
Разницей множеств A и B принято называть отдельное множество C = A | B, которое содержит все элементы A, которые не являются элементами, принадлежащими множеству B.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Виды чисел

В математике все числа разделяются на 7 разных видов:

1. натуральные – N;
2. натуральные, включающие нуль – N_{0};
3. целые – Z;
   • целые отрицательные – Z^{-};
   • целые положительные – Z^{+};
4. иррациональные;
5. рациональные – Q;
6. комплексные – C;
7. действительные – R.

Рассмотрим более подробно каждый из перечисленных видов чисел:

Основным отличием натуральных чисел является то, что они применяются при перечислении различных предметов или естественном счете. Проще говоря, при нумерации – «первый», «второй», «третий», «четвертый» и т.п. Множество натуральных чисел описывается следующим образом: N={1,2,3,4,5, ….}.

Натуральными числами, включающими нуль обозначаются определенные количества каких-либо предметов: N={0,1,2,3,4,5…}.

Целыми называют числа, входящие в числа с отрицательными и положительными знаками:

обозначение целых отрицательных чисел выглядит следующим образом: Z^{- }и пишется Z^{-}=N={…,-5,-4,-3,-2,-1};

целые положительные числа в свою очередь обозначаются Z^{+} и записывается Z^{+}=N={1,2,3,4,5…}.

Иррациональными называют вещественные числа, которые на являются рациональными и не могут никогда представляться в виде десятичных дробей.

Рациональными называют те числа, которые можно представить в виде обыкновенной дроби, имеющей вид m/n, где m и n — это целые числа, а \[n \neq{0}\]. Для обозначения рациональных чисел в математике используется большая буква Q.

При переводе в десятичную дробь каждое рациональное число может представляться в виде бесконечной или конечной дроби.

Комплексными принято называть числа, в которых содержится мнимая единица i.

Действительные числа также называют вещественными. В них объединяются два вида чисел: рациональные (R) и иррациональные.

Примеры задач по определению множества чисел