Нахождение координат середины отрезка: примеры, решения

Основное определение отрезка

Прямую АВ можно получить путем удлинения отрезка, который состоит из двух точек. Вследствие чего, можно сказать, что полученный отрезок АВ — это часть прямой, которая ограничена точками А и В. Отрезок объединяет обе точки, которые являются концами прямой, а также множество других точек, лежащих на отрезке.  

Например: дана точка К которая расположена между заданными отметками, следовательно, можно сказать, что данная точка лежит на этом отрезке.

Середина отрезка на координатной прямой

Заданы следующие параметры: координатная прямая Ox; точки А и В, которые не совпадают с данной прямой.

Заданным точкам соответствуют действительные числовые значения \[x_{A}\] и \[x_{B}\]. Координата С — это середина отрезка А и В. Исходя из этого нужно определить значение координаты \[x_{C}\] .

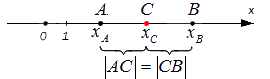
AB = |a — b|, где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.

Середина отрезка на плоскости

Зададим следующие параметры: прямоугольная система координат относительно заданной плоскости Oxy; две произвольно расположенные несовпадающие точки, для которых заданы координаты \[\mathrm{A}\left(x_{A} y_{A}\right)\] и \[B\left(\chi_{B} \chi_{B}\right)\]. Точка C — это заданная середина отрезка АВ. Нужно вычислить координаты \[x_{C}\] и \[y_{C}\] относительно точки С.

Чтобы правильно проанализировать задачу, возьмем случай, когда точки A и В между собой не совпадают и расположены на одной координатной плоскости.

В свою очередь координатная плоскость является перпендикулярной относительной одной из осей.

Координаты отметок \[A_{x} A_{y} B_{x} B_{y} C_{x} C_{y}\] — это проекции точек А, В, С.

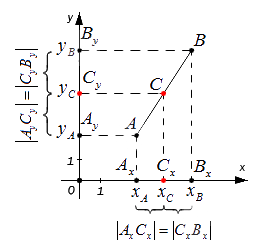
Согласно построению, все прямые можно назвать параллельными; прямые также параллельны между собой. Принимая во внимание данное свойство и теорему Фалеса из равенства А С   =   С В следуют, что все  равенства между собой равны. Также они в свою очередь свидетельствуют о том, что точка \[C_{x}\] – это середина отрезка \[A_{x}\] и \[B_{x}\], \[C_{y}\] а – середина отрезка \[A_{y}\] и \[B_{y}\].

Опираясь на полученное выражение получаем основное уравнение середины отрезка на координатной плоскости. 

Данным набором формул можно использовать, когда точки А и B лежат на одной координатной плоскости или прямой. Которая соответственно перпендикулярна относительной одной из осей.

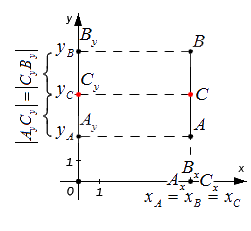
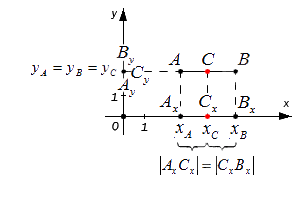
В данном случае координаты отрезка будут определяться по следующей формуле:

Параметры середины отрезка в пространстве

Для выведения основной формулы для решения подобного рода задач, нужно рассмотреть конкретный пример.

Дана система координат, две произвольные координатные точки с конкретными координатами \[\mathrm{A}\left(A_{x} A_{y} A_{z}\right)\] и \[\mathrm{B}\left(B_{\chi} B_{y} B_{z}\right)\]. Нужно определить отметку точки C, которая в свою очередь будет являться серединой отрезка.

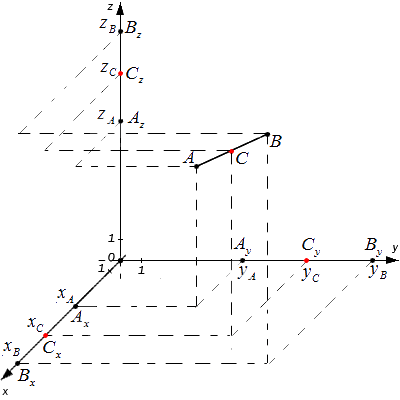
Согласно основной теоремы Фалеса, все равенства между собой являются равными. Следовательно, значение точек С будут являться серединами отрезков, каждой координатной плоскости, коих имеется три.

Можно составить и записать окончательную формулу для определения середины прямой при координатной плоскости, состоящей более чем двух осей.

Данные формулы также можно применять в случаях, когда точки A и B расположены на одной из координатных прямых. Либо на прямой, которая перпендикулярна относительно одной из осей. Есть еще случай, когда точки расположены в одной координатной плоскости, которая перпендикулярна одной из координатных плоскостей.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для определения отметок середины отрезка, можно определить применяя алгебраическое правило решения векторных выражений.

Исходные данные: прямоугольная декартова система координат Oxy, точки с конкретно заданными координатами \[\mathrm{A}\left(A_{x} A_{y}\right)\] и \[\text { B }\left(B_{x} B_{y}\right)\].

Точка  C – это середина отрезка с точками А и В.

Согласно геометрическому правилу и определению, действия над векторами будет выглядеть следующим образом:

Координата С в данной ситуации — это значение, в которой пересекаются диагонали геометрической фигуры параллелограмм. Данная фигура построена на основании следующих векторов  \[\overline{O A}\] и \[\overline{O B}\], иными словами — это точка середины диагоналей.

Координатные показатели радиуса — это векторные показатели, которые  равны координатам, тогда будут верны и равенства: \[\overline{O A}\left(x_{A} y_{A}\right)\] и \[\overline{O B}\left(x_{B} y_{B}\right)\].

Выполним следующие действия над векторными значениями и получим следующие формулы:

Следовательно, заданная координата С обладает данными:

Аналогичным образом определяется нахождение координат середины заданного отрезка в пространстве.

Примеры решения задачи, при нахождении точки середины отрезка