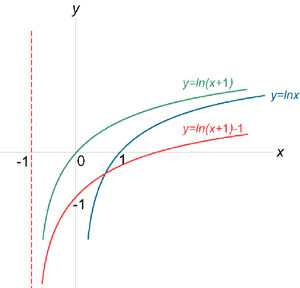Натуральный логарифм числа

Оглавление

Время чтения: 4 минуты

1 672

Натуральный логарифм числа
Свойства натурального логарифма
Описание функции натурального логарифма
График натурального логарифма

Натуральный логарифм числа

Определение

Под определением натурального логарифма принято считать логарифмическое значение по основанию к иррациональному значению.

Обозначается натуральный логарифм в виде значения:

ln или \[\log _{e} x\].

Зачастую значение числа x под знаком логарифма является вещественным значение, либо его еще принято называть комплексным числом.

Формулы натурального логарифма:

\[ \ln =0 \]

\[ \ln (x y)=\ln x+\ln y \]

\[ \ln \frac{x}{y}=\ln x-\ln y \]

\[ \ln x^{n}=n \cdot \ln x \]

Свойства натурального логарифма

Из основного определения логарифма можно сформулировать главное логарифмическое тождество (уравнение).

e^lna=a

Для равенства двух простых натуральных логарифмов следует равенство логарифмируемых значений выражения.
В случае, когда возрастает значения любого аргумента, следовательно, будет возрастать и логарифмическое значение функции.

Описание функции натурального логарифма

Логарифмическая функция выражается как: y=log n^k

Где значение n, имеет значение больше нуля и не менее единицы.

Область определения логарифма и функции — это совокупность положительных значений и действительных чисел.

Рассмотрим на примере, характер решения задачи данной функции.

Пример №1:

y = ln x, вычислить область определения.

\[\mathrm{D}(\mathrm{y})=(0 ;+\infty)\]

На заданном интервале, производная будет иметь положительное значение, и функция будет возрастать на всем промежутке.

\[ y=\ln x=\frac{1}{x}; \]

Определим односторонний предел при, стремлении аргумента к нулю и когда значение x стремится к бесконечности.

\[ \lim _{x \rightarrow 0+0} \ln x=\ln (0+0)=-\infty; \]

\[ \lim _{x \rightarrow \infty} \ln x=\ln (+\infty)=+\infty. \]

Из данного решения мы видим, что значения будут возрастать от минус бесконечности до плюс бесконечности.

Из этого следует, что множество всех действительных чисел – является областью значений функции натурального логарифма ln.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

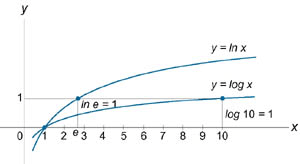
График натурального логарифма

Значение логарифма принято обозначается при положительных числовых значениях переменной x. Затем он монотонно начинает возрастать по всей своей области определения.

При значении, которое стремится к нулю (x → 0) пределом натурального логарифма, будет считаться значение до бесконечности с отрицательным значением ( – ∞ ).

Для значений x, которые имеют большие значения, логарифм возрастает относительно медленно.

Значение степенной функции xⁿ, имея при этом положительное значение показателя степени, будет возрастать намного быстрее, чем сама функция.

Ниже приведены рисунки графического изображения функции.