Примеры решения производных с ответами
Производные значения функций
Производная функции — это основное понятие дифференциального исчисления значений.
Как правило производная характеризует с какой скоростью изменяется функция в конкретной точке. Производные используются в большинстве видов задач не только в математике, но и других технических науках.
Для решения задач с производными функциями существует стандартный перечень основных производных.
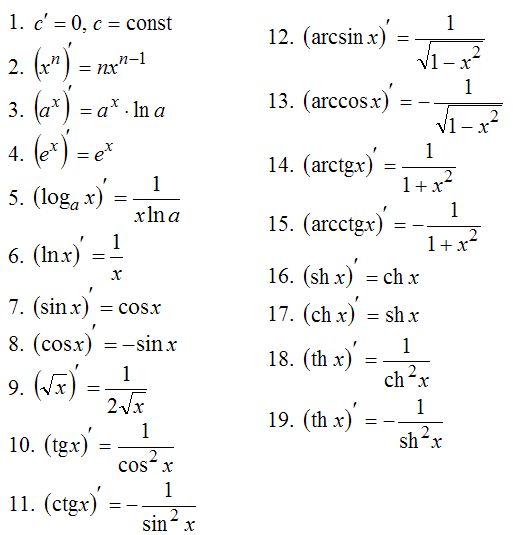
Подробное решение производных уравнений
Пример №1:
Нужно вычислить производную заданной функции \[y=2^{x}-\operatorname{arctg} x\].
Согласно основным правилам производной, при которой производная суммы значений функции равняется сумме производной.
Используя формулу производной составим уравнение и решим его:
Применяя формулы производных и обратных тригонометрических функций решим уравнение:
Ответ: \[y^{\prime}=2^{x} \ln 2-\frac{1}{1+x^{2}}\].
Пример №2:
Нужно вычислить приблизительное значение заданной функции arctg 1.02. При этом производя замену приращения функции ее дифференциалом.
Рассмотрим подробно функцию y= arctg x.
Для данной функции нужно вычислить значение в точке равной 1,02.
Для этого выразим функцию в следующем выражении: \[x=x_{0}+\Delta x\].
Значения двух точек \[\mathrm{x}_{0}\] и \[\Delta x\] подбираются таким образом, чтобы при вычислении значений функции и ее производных было легко проводить расчеты. При этом желательно числа выбирать так, чтобы значение \[\Delta x\]. было достаточно минимальным по значению.
Учитывая все требования можно сделать следующий вывод:
\[x=1.02=1+0.02\] , а именно \[ x_{0}=1 \text { и } \Delta x=0,02 .\]
Определим значения для заданной функции y= arctg x в первой точке равной \[\mathrm{x}_{0} = 1\]
\[y\left(x_{0}\right)=y(1)=\operatorname{arctg} 1=\frac{\pi}{4}\].
Следующим действием проведем дифференциацию заданного выражения и вычисли значение функции \[y^{\prime}=(\operatorname{arctg} x)^{\prime}=\frac{1}{1+x^{2}}\] из этого следует, что \[y^{\prime}(1)=\frac{1}{2}\].
Составим и решим окончательное уравнение и найдем его значение:
\[y(1,02)=\operatorname{arctg} 1,02=y(1+0,02) \approx y(1)+y^{\prime}(1) \cdot \Delta x=\frac{\pi}{4}+\frac{1}{2} \cdot 0,02 \approx 0,7852+0,01=0,7952\]
Ответ: \[\operatorname{arctg} 1,02 \approx 0,7952\]
Пример №3:
Согласно заданию, необходимо определить производную для функции \[y=x^{3}+\sin x+\ln x\].
Так как производное значение равняется сумме производных составим выражение.
\[y^{\prime}=\left(x^{3}+\sin x+\ln x\right)^{\prime}=\left(x^{3}\right)^{\prime}+(\sin x)^{\prime}+(\ln x)^{\prime}\]
Для дальнейшего решения необходимо воспользоваться таблицей производных и выбрать нужную функцию, которая будет подходить под данное решение.
\[y^{\prime}=3 x^{3-1}+\cos x+\frac{1}{x}\], преобразуем уравнение и получим упрощенный вид уравнения и выполним его решение:
\[y^{\prime}=3 x^{2}+\cos x+\frac{1}{x}\].
Ответ: \[y^{\prime}=3 x^{2}+\cos x+\frac{1}{x}\].
Пример №4:
Дана функция \[y=\frac{3 x-1}{2 x+5}\].
Необходимо определить ее производную применяя таблицу функций.
Составим уравнение функции используя дифференцирование. И получим следующее выражение:
Принимая во внимание все основные правила при решении функций и производных делаем вывод, что постоянное значение константы можно перенести за знак самой производной:
Ответ: \[y^{\prime}=\frac{17}{(2 x+5)^{2}}\]
Пример №5:
Для функции \[y=\frac{\cos x}{x^{3}+1}\] нужно определить производную.
Нужно применить правило дифференцирования частного значения и составить уравнение:
Последующее решение необходимо выполнять, руководствуясь ранее изученными правилами производной функции.
В ходе решения нужно выбрать правильную производную функцию и используя ее решить уравнение:
Ответ: \[y^{\prime}=\frac{-\sin x \cdot\left(x^{3}+1\right)-3 x^{2} \cdot \cos x}{\left(x^{3}+1\right)^{2}}\]
Пример №6:
Нужно вычислить производную для функции \[y=\frac{x^{3}}{\ln x}\]
Начинаем порядок решения с правила дифференцирования частного значения:
Затем используем известные формулы производных, логарифмических значений и степеней. Составляем и решаем следующее уравнение:
Ответ: \[y^{\prime}=\frac{x^{2}(3 \ln x-1)}{\ln ^{2} x}\]
Пример№ 7:
Вычислить производную для функции \[y=3 x^{2}+5 \sqrt[3]{x^{5}}-\frac{4}{x^{3}}\]
Для решения необходимо применять производную подходящую для данной функции и помнить правило суммы.
Множитель, который является постоянным по значению можно перенести за знак производной и получим выражение:
Далее необходимо применить формулу и рассчитать значение производной для функции со степенью.
Ответ: \[y^{\prime}=6 x+\frac{25}{3} \sqrt[3]{x^{2}}+\frac{12}{x^{4}}\]















