Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной
Касательная к графикам функции в точке
Угол наклона прямой линии \[y=k x+b\] — это угол \[a\], который берет свой отсчет от положительного направления оси координат ox по направлению к прямой. Угол наклона может иметь значение как со знаком плюс, так и со знаком минус.
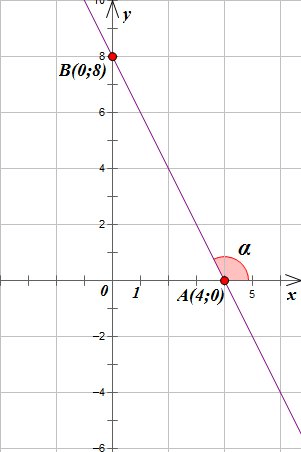
На расположенном рис.1 показана прямая и угол наклона относительно оси.
Для каждого угла наклона характерен угловой коэффициент прямой.
Угловой коэффициент — это числовой коэффициент прямой вида \[\boldsymbol{y=k x+b}\]. В уравнение он обозначается буквой k.
Угловой коэффициент равен значению тангенса наклона заданной прямой линии: \[k=\operatorname{tg} \alpha\].
Основные значения угла наклона прямой
- Угол наклона прямой линии будет иметь нулевое значение, только в случае, когда параллельна ось Ox, и значение углового коэффициента равняется нулю. Потому что \[\operatorname{tg} 0=0\]. Следовательно уравнение прямой будет записываться следующим образом: \[y=b\].
- В случае, когда угол наклона будет острым, то должно выполняться два следующих условия: \[0<\alpha<\frac{\pi}{2}\] или \[0^{\circ}<\alpha<90^{\circ}\]. Отсюда следует, что значение углового коэффициента будет являться положительным значением. Потому что значение тангенса удовлетворяет следующему условию, где показатель тангенса больше нулевого значения: \[t g>0\]. При этом будет наблюдаться возрастание графика функции на протяжении всей координатной прямой.
- При условии, что угол \[\alpha=\frac{\pi}{2}\], из этого следует, что прямая будет располагаться относительно оси Ox в перпендикулярном положении. Условие задается следующим равенством \[x=c\]. Где с — это простое действительное число.
- Если угол наклона прямой, является тупым, то будет применяться следующее условие: \[\frac{\pi}{2}<\alpha<\pi\] или \[90^{\circ}<\alpha<180^{\circ}\] . Для данного случая характерно отрицательное значение углового коэффициента и убывание функции.
Секущая прямая — это прямая, которая проходит через две точки заданной функции. Иными словами, можно сказать, что секущая — это прямая, которую можно провести через две любые точки графика.
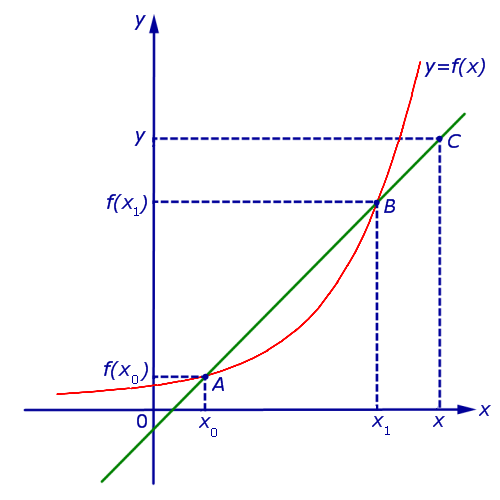
На графике показана секущая, которая обозначена красным цветом и точками А и В.
Если угловой коэффициент прямой линии равен тангенсу угла наклона, то используя прямоугольный треугольник можно найти значение тангенса. Сделать это можно вычислением по правилу: тангенс равен отношению противолежащего катета к прилежащему.
Чтобы определить значение секущий, нужно использовать следующую формулу:
\[k=\operatorname{tg} \alpha=\frac{B C}{A C}=\frac{f\left(\chi_{B}\right)-f\left(\chi_{A}\right)}{\chi_{B}-\chi_{A}}\], где:
\[\chi_{B}, \chi_{A}\] — абсциссы точек А и В;
\[f\left(\chi_{B}\right), f\left(\chi_{A}\right)\] — значения функции, в заданных точках.
Значение секущий определяется, используя следующее неравенство:
\[k=\frac{f\left(\chi_{B}\right)-f\left(\chi_{A}\right)}{\chi_{B}-\chi_{A}}\] либо \[k=\frac{f\left(\chi_{A}\right)-f\left(\chi_{B}\right)}{\chi_{A}-\chi_{B}}\]
Уравнение записывается следующим образом:
Касательная к графику функции — это прямая, которая проходит через определенную заданную точку, которая в свою очередь имеет отрезок с множеством числовых значений x.
Пример:
Прямая задана следующей функцией: \[y=x+1\]. Данная функция считается касательной к графику \[y=2 \sqrt{x}\] с координатными точками (1;2).
Рассмотрим графики со значениями (1;2). Функция обозначается черным цветом, а касательная линия соответственно синим цветом.
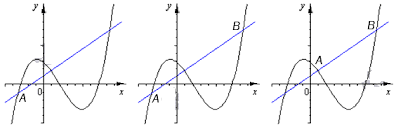
Чтобы определить касательную к функции, нужно исследовать поведение касательной АВ. При этом должно быть бесконечное приближение точки В к точке А.
Значение производной функции в точке и ее геометрический смысл
Для заданной функции \[f(\chi)\] рассмотрим секущую АВ. Точки А и В заданы следующими значениями: \[\left(\chi_{0}, f\left(\chi_{0}\right)\right)\] и \[\left(\chi_{0}+\Delta \chi ,\left(\chi_{0}+\Delta \chi\right)\right.\].
\[\Delta \chi\] — это показатель приращения значения аргумента.
Подставив все значения в исходную функцию получим следующий вид:
\[\Delta y=\Delta f(\chi)=f\left(\chi_{0}+\Delta \chi\right)-f(\Delta \chi)\].
Для более лучшего восприятия решения, построим график.
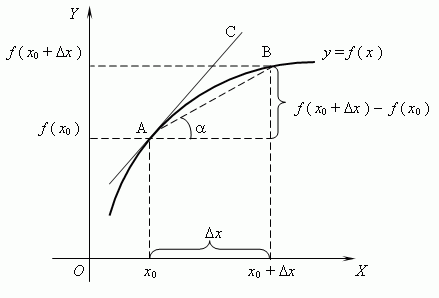
Из графика видно, что образуется прямоугольный треугольник ABC. Составим соотношение \[\frac{\Delta y}{\Delta x}=\operatorname{tg} \alpha\], для этого необходимо применить основное определение тригонометрической функции, а именно тангенса.
Исходя из основного определения касательной, запишем следующее выражение:
Используя правило производной, имеем следующее:
- производная \[f(x)\] в точке \[x_{0}\] — является пределом отношения приращения функции к аргументу.
- \[\Delta_{\chi} \rightarrow 0 \text { и } f\left(x_{0}\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}\].
Следовательно:
\[k_{z}\] — это угловой коэффициент касательной функции.
Из данной функции можно сделать следующий вывод:
- функция \[f(x)\] может находится в точке со значением \[x_{0}\]
- функция может быть касательной к графику в некой точке касания, где угловой коэффициент равняется производной.
Понятие уравнения касательной прямой
Чтобы составить уравнение прямой, нужно знать угловой коэффициент с заданной точкой. Это точка, через которую проходит прямая. При пересечении угловой коэффициент записывается как значение \[x_{0}\].
Уравнение касательной записывается следующим образом:
График функции \[y=f(x)\].
Расположение касательной прямой непосредственно зависит от значения углового коэффициента. Если прямая параллельна оси Ox, то значение коэффициента равно нулевому значению. При параллельном расположении относительно оси Oy, коэффициент угловой принимает значение бесконечности. При это уравнение касательной записывается как: \[x=x_{0}\].Также угловой коэффициент будет возрастать при значении больше нуля, а если коэффициент меньше нуля, то функция соответственно будет убывать.
Нужно составить уравнение касательной к графику функции.
\[y=e^{x+1}+\frac{x^{3}}{3}-\frac{6-\sqrt{3}}{3} x-\frac{17-\sqrt{3}}{3}\]
Порядок решения:
Из условия задачи следует, что функция может быть определенной для всех действительных значений. Точка,
которая задана с координатами (1;3) будет являться точкой касания, следовательно , \[x_{0}=-1,
f\left(x_{0}\right)=-3\].
Для точки со значение равным -1, нужно определить производную.
Для этого составим уравнение:
\[y^{\prime}=\left(e^{x+1}+\frac{x^{3}}{3}-\frac{6-\sqrt{3}}{3}
x-\frac{17-\sqrt{3}}{3}\right)^{\prime}=\\\left(e^{x+1}\right)^{\prime}+\left(\frac{x^{3}}{3}\right)^{\prime}-\left(\frac{6-\sqrt{3}}{3}
x\right)^{\prime}-\left(\frac{17-\sqrt{3}}{3}\right)^{\prime}=e^{x+1}+x^{2}-\frac{6-\sqrt{3}}{3};\]
\[y^{\prime}\left(x_{0}\right)=y^{\prime}(-1)=e^{-1+1}+(-1)^2-\frac{6-\sqrt{3}}{3}=\frac{\sqrt{3}}{3}\]
Показатель \[f^{\prime}(x)\] в точке, которая является касательной, будет равен угловому коэффициенту.
Угловой коэффициент равен наклону тангенса. Отсюда следует, что:
\[k_{x}=\operatorname{tg} \alpha_{x}=y^{\prime}\left(x_{0}\right)=\frac{\sqrt{3}}{3}\Rightarrow \alpha_{\chi}=\operatorname{arctg} \frac{\sqrt{3}}{3}=\frac{\pi}{6}\]
Подведем итоги, и запишем ответ:
\[y=f^{\prime}\left(x_{0}\right) \cdot\left(x-x_{0}\right)+f\left(x_{0}\right);\\y=\frac{\sqrt{3}}{3}(x+1)-3
; y=\frac{\sqrt{3}}{3} x-\frac{9-\sqrt{3}}{3}\]
По условию задачи нужно определить касательную к графику функции \[y=3 \cdot \sqrt[5]{x-1}+1\]. Точки
координат равны (1;1). Также нужно составить уравнение и определить значение угла наклона.
Согласно условию задачи, область определения функции — это простые действительные числа.
Определим значение производной.
\[y^{\prime}=(3 \cdot \sqrt[5]{x-1}+1)^{\prime}=3 \cdot \frac{1}{5} \cdot(x-1)^{\frac{1}{5}} 1=\frac{3}{5}
\cdot \frac{1}{(x-1)^{\frac{4}{5}}}\]
При условии, что \[x_{0}=1\] тогда функция будет не определенной, но пределы ее можно записать как:
\[\lim _{x \rightarrow 1+0}\left(\frac{3}{5} \cdot \frac{1}{(x-1)^{\frac{4}{5}}}\right)=\frac{3}{5} \cdot
\frac{1}{(+0)^{\frac{4}{5}}}=\frac{3}{5} \cdot \frac{1}{+0}=\infty\]
\[\lim _{x \rightarrow 1-0}\left(\frac{3}{5} \cdot \frac{1}{(x-1)^{\frac{4}{5}}}\right)=\frac{3}{5} \cdot
\frac{1}{(-0)^{\frac{4}{5}}}=\frac{3}{5} \cdot \frac{1}{+0}=+\infty\]
Это значит, что вертикальная касательная в точке существует.
Ответ: после всех проведенных вычислений уравнение приобретает вид x=1, где угол наклона будет равен
\[\frac{\pi}{2}\].

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Касательная линия к окружности
Для того чтобы задать окружность с центром в следующих точках:
\[\text {(Xcenter;Ycenter)}\] и радиусом R, нужно воспользоваться формулой.
\[(x-x_{center})^2+(y+y_{center})^2=R^2\]
Данное выражение можно представить как две функции:
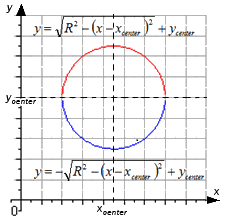
Из рисунка видно, что первая функция расположена в верхней части координатной плоскости. Вторая функция, соответственно в нижней части.
Чтобы составить уравнение окружности в точке, которая находится в верхней или нижней полуокружности, нужно составить уравнение для графика функции следующего вида:
\[y=\sqrt{R^{2}-\left(x-x_{\text {center }}\right)^2 +y_{\text {center }}}\] и \[y=-\sqrt{R^{2}-\left(x-x_{c e n t e r}\right)+y_{c e n t e r}}\], для конкретной точки.
Если в точках (xcenter;ycenter +R) и (xcenter;ycenter -R) касательные к окружности задаются выражением \[y=y_{\text {center }}+R \] и \[y=y_{\text {center }}-R\], то они будут параллельны оси Oy. Из этого следует следующее уравнение \[x=x_{\text {center }}+R\] и \[x=x_{\text {center }}-R\].
Касательная к геометрической фигуре эллипс
Геометрическая фигура эллипс может быть задана следующей функцией:
Данное уравнение можно применять при следующих условиях:
- эллипс имеет в центре следующие точки: xcenter; ycenter
- a и b — это значение полуосей.
Используя два вида функций можно обозначить эллипс и окружность:
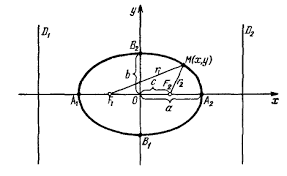
Необходимо составить уравнение касательной к эллипсу \[\frac{(x-3)^2}{4}+\frac{(y-5)^2}{25}=1\]. При этом
значение точки x будет равняться двум.
Порядок решения задачи:
Нужно определить точки касания, которые приближены к значению равным двум.
В уравнение подставляем данные.
\[\left|\left(\frac{(x-3)^{2}}{4}\right)\right|_{x=2}+\frac{(y-5)^{2}}{25}=1\]
\[\frac{1}{4}+\frac{(y-5)^{2}}{25}=1 \Rightarrow(y-5)^{2}=\frac{3}{4} \cdot 25 \Rightarrow y=\pm \frac{5
\sqrt{3}}{2}+5\]
Точки касания, принадлежащие верхнему и нижнему полуэллипсу:
\[\left(2 ; \frac{5 \sqrt{3}}{2}+5\right) и \left(2 ;-\frac{5 \sqrt{3}}{2}+5\right)\].
Составим уравнение эллипса для координатной оси Oy.
\[\frac{(x-3)^{2}}{4}+\frac{(y-5)^{2}}{25}=1\];
\[\frac{(y-5)^{2}}{25}=1-\frac{(x-3)^{2}}{4}\];
\[(y-5)^{2}=25 \cdot\left(1-\frac{(x-3)^{2}}{4}\right)\];
\[y-5=\pm 5 \cdot \sqrt{1-\frac{(x-3)^{2}}{4}};\]
\[y=5 \pm \frac{5}{2} \sqrt{4-(x-3)^{2}}\];
Функция верхнего полуэллипса будет задаваться следующим видом:
\[y=5+\frac{5}{2} \sqrt{4-(x-3)^{2}}\];
Нижний полуэллипс можно записать как:
\[y=5-\frac{5}{2} \sqrt{4-(x-3)^{2}}\].
Для того чтобы составить уравнение касательной в точке, нужно применить стандартный алгоритм решения.
Для первой касательной в точке \[\left(2 ; \frac{5 \sqrt{3}}{2}+5\right)\] уравнение будет выглядеть
следующим образом:
\[y^{\prime}=\left(5+\frac{5}{2} \sqrt{4-(x-3)^{2}}\right)^{\prime}=\frac{5}{2} \cdot \frac{1}{2
\sqrt{4-(x-3)^{2}}} \cdot\left(4-(x-3)^{2}\right)^{\prime}=\\=-\frac{5}{2} \cdot
\frac{x-3}{\sqrt{4-(x-3)^{2}}} \Rightarrow y^{\prime}\left(x_{0}\right)=y^{\prime}(2)=-\frac{5}{2} \cdot
\frac{2-3}{\sqrt{4-(2-3)^{2}}}=\frac{5}{2 \sqrt{3}} \Rightarrow\\y=y^{\prime}\left(x_{0}\right)
\cdot\left(x-x_{0}\right)+y_{0} \Rightarrow y=\frac{5}{2 \sqrt{3}}(x-2)+\frac{5}{2 \sqrt{3}}+5\]
Для второй касательной с точкой функция будет иметь следующий вид:
\[y^{\prime}=\left(5-\frac{5}{2} \sqrt{4-(x-3)^{2}}\right)^{\prime}=-\frac{5}{2} \cdot \frac{1}{2
\sqrt{4-(x-3)^{2}}} \cdot\left(4-(x-3)^{2}\right)^{\prime}=\\=\frac{5}{2} \cdot
\frac{x-3}{\sqrt{4-(x-3)^{2}}} \Rightarrow y^{\prime}\left(x_{0}\right)=y^{\prime}(2)=-\frac{5}{2} \cdot
\frac{2-3}{\sqrt{4-(2-3)^{2}}}=-\frac{5}{2 \sqrt{3}} \Rightarrow\\y=y^{\prime}\left(x_{0}\right) \cdot\left(x-x_{0}\right)+y_{0} \Rightarrow y=-\frac{5}{2 \sqrt{3}}(x-2)-\frac{5}{2 \sqrt{3}}+5\]
Касательная к гиперболе. Основные функции
Чтобы составить уравнение касательной к геометрической фигуре гипербола, нужно применять основной алгоритм решения задач подобного типа.
Для гиперболы будет характерно следующее неравенство:
При этом должны выполняться следующие условия:
- центр в точке xcenter;ycente
- вершины точки (xcenter+ \[a\]; ycenter) и (xcenter-\[a\]; ycenter)
Если вершины имеют значения: (xcenter;ycenter+b) и (xcenter;ycenter-b), то функция задается следующим образом: \[\frac{\left(x-x_{\text {center }}\right) 2}{a^{2}}+\frac{\left(y-y_{\text {center }}\right) ^2}{b^{2}}=-1\].
Гиперболу можно определить, используя две пары уравнений, которые записываются в следующем виде:
или
Для первых уравнение характерно параллельное расположение касательной относительно оси Oy. Соответственно для второй пары уравнений: параллельное расположение относительно оси Ox.
Составим уравнение касательной к гиперболе следующего вида: \[\frac{(x-3)^{2}}{4}-\frac{(x+3)^{2}}{9}\], в
характерных точках \[(7 ;-3 \sqrt{3}-3)\].
Преобразование заданное уравнение при помощи двух функций.
\[\frac{(x-3)^{2}}{4}-\frac{(x+3)^{2}}{9}=1 \Rightarrow \frac{(x+3)^{2}}{9}=\frac{(x-3)^{2}}{4}-1
\Rightarrow(y-3)^{2}=\\9 \cdot\left(\frac{(x-3)^{2}}{4}-1\right) \Rightarrow y+3=\frac{3}{2} \cdot \sqrt{(x-3)^{2}-4}\] или \[y+3=-\frac{3}{2}\]
\[\sqrt{(x-3)^{2}-4} \Rightarrow\\y=\frac{3}{2} \cdot \sqrt{(x-3)^{2}-4}-3\\y=-\frac{3}{2} \cdot \sqrt{(x-3)^{2}-4}-3\]
Далее нужно определить к какой из двух функций относится точка с координатами: \[(7 ;-3 \sqrt{3}-3)\].
Проверим первую функцию \[y(7)=\frac{3}{2} \cdot \sqrt{(7-3)^{2}-4}-3=3 \sqrt{3}-3 \neq-3 \sqrt{3}-3\], из уравнения следует, что заданная точка не принадлежит графику, потому что равенство не выполняется.
Следовательно, нужно определить угловой коэффициент:
\[y^{\prime}=\left(-\frac{3}{2} \cdot \sqrt{(x-3)^{2}-4}-3\right)^{\prime}=-\frac{3}{2} \cdot \frac{x-3}{\sqrt{(x-3)^{2}-4}} \Rightarrow\\k_{x}=y^{\prime}\left(x_{0}\right)=\left(-\frac{3}{2} \cdot \frac{x_{0}-3}{\sqrt{\left(x_{0}-3\right)^{2}-4}}\right)=-\frac{3}{2} \cdot \frac{7-3}{\sqrt{(7-3)^{2}-4}}=-\sqrt{3}\]
Ответ: уравнение касательной записывается следующим образом: \[y=-\sqrt{3} \cdot(x-7)-3 \sqrt{3}-3=-\sqrt{3} \cdot x+4 \sqrt{3}-3\]
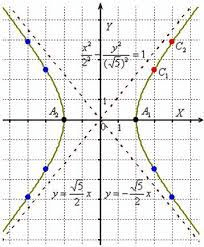
Касательная к параболе. Основные правила решения
Используя стандартный алгоритм решения, можно составить уравнение касательной к параболе \[y=a x^{2}+b x+c\] в точках \[\left(x_{0}, y\left(x_{0}\right)\right)\]. Данное уравнение после преобразования будет иметь следующий вид:
\[y=y^{\prime}\left(x_{0}\right) \cdot\left(x-x_{0}\right)+y\left(x_{0}\right)\].
Необходимо задать параболу \[x=a y^{2}+b y+c\] как общая функция двух уравнений. Затем решить уравнение относительно оси Oy.
Чтобы определить принадлежность заданных точек \[\left(x_{0}, y\left(x_{0}\right)\right)\], необходимо руководствоваться стандартным решением согласно алгоритма. Данная касательная будет иметь параллельное расположение относительно параболы.
Необходимо составить уравнение к графику касательной: \[x-2 y^{2}-5 y+3\] при угле наклона равным \[150^{\circ}\]
Для решения будем применять стандартный алгоритм решения задач.
Для начала данную параболу нужно расписать и составить две функции, следующего вида:
\[-2 y^{2}+5 y+3-x=0;\\D=(-5)^{2}-4 \cdot(-2) \cdot(3-x)=49-8 x;\\y=\frac{5+\sqrt{49-8 x}}{-4};\\y=\frac{5-\sqrt{49-8 x}}{-4}.\]
Значение углового коэффициента будет равняться значению производной в конкретной точке \[x_{0}\] для этой функции. И будет равен значению тангенса угла наклона.
\[k_{x}=y^{\prime}\left(x_{0}\right)=\operatorname{tg} \alpha_{x}=\operatorname{tg} 150^{\circ}=-\frac{1}{\sqrt{3}}\];
Из уравнения сможем определить значение x для всех точек касания.
Функции будут записываться следующим образом:
\[y^{\prime}=\left(\frac{5+\sqrt{49-8 x}}{-4}\right)^{\prime}=\frac{1}{\sqrt{49-8 x}} \Rightarrow y^{\prime}\left(x_{0}\right)=\\\frac{1}{\sqrt{49-8 x_{0}}}=-\frac{1}{\sqrt{3}} \Leftrightarrow \sqrt{49-8 x_{0}}=-\sqrt{3}\]
В данном уравнении действительных корней нет. Так как ответ получился отрицательный.
Отсюда делаем вывод, что касательной линии с углом равным \[150^{\circ}\] для функции такого вида не существует.
Функция второго вида:
\[y^{\prime}=\left(\frac{5-\sqrt{49-8 x}}{-4}\right)^{\prime}=-\frac{1}{\sqrt{49-8 x}} \Rightarrow y^{\prime}\left(x_{0}\right)=-\frac{1}{\sqrt{49-8 x_{0}}}=\\-\frac{1}{\sqrt{3}} \Leftrightarrow \sqrt{49-8 x_{0}}=-\sqrt{3}\\x_{0}=\frac{23}{4} \Rightarrow y\left(x_{0}\right)=\frac{5-\sqrt{49-8 \cdot \frac{23}{4}}}{-4}=\frac{-5+\sqrt{3}}{4}\]
Точки касания: \[\left(\frac{23}{4} ; \frac{-5+\sqrt{3}}{4}\right)\].
Ответ: уравнение касательной имеет вид: \[y=-\frac{1}{\sqrt{3}} \cdot\left(x-\frac{23}{4}\right)+\frac{-5+\sqrt{3}}{4}\].















