Простые и составные числа
Что представляют собой простые и составные числа. Делитель простого и составного числа
Все натуральные числа (исключение составляет лишь единица) относятся к простым или составным. При этом, основным различием между двумя большими группами чисел является количество делителей. Делители, также, подразделяются на составные и простые. Чтобы само определение составных чисел было более понятным, можно предварительно просмотреть понятия делителей и кратных.
Простыми числам являются натуральные числа больше единицы, имеющие два положительных делителя – себя и 1. Например, делителем чисел 7, 11, 19, 131 выступает только единица и само число.
Составными числами являются натуральные числа больше единицы, но в отличие от простого, они имеет больше положительных делителей — оно делится на единицу, на само себя и, как минимум, на одно натуральное число. Например, разложение составных чисел на делители можно представить следующим образом — число 14 делиться на 1, 2, 7, 14, а число 24 делиться на 1,2, 3, 8, 12, 6, 4.
Так, число 2 является единственным первым наименьшим четным простым числом. Все остальные простые числа принадлежат к нечетной группе. А в числовом ряду составных чисел наименьшим первым числом выступает 4. В числовом ряду можно выделить первые составные и простые числа, но определить последние числовые значения невозможно.
Следует обратить внимание на число 1 – оно занимает особое место, поскольку не относится ни к составным, ни к простым числам. Наличие единственного простого делителя – единицы, является главным отличием от остальных натуральных чисел.
Любое натуральное число n больше единицы представляет простые или составные числа. Учитывая свойства делимости, можно подытожить, что единица и в всегда будут являться делителями любого числа в. То есть, любое число, кроме 1, будет иметь минимум два делителя — единицу и самого себя.
Учитывая все вышесказанное, можно дать следующие определения. Простыми являются числа, натуральное числовое значение, которое обладает только двумя положительными делителями. Составными являются числа – это натуральное числовое значение, которое обладает минимально тремя положительными делителями.
Так, любое число, которое не будет причислено к составным, можно отнести к простым числам. Исключение составляет лишь единица.
Таблица простых чисел
Часто, при выполнении различных заданий, оптимальным решением станет использование таблицы простых чисел. Так как простых чисел множество, таблицы обычно ограничиваются числовым значением 100, 1000 или 10 000. Так, на Рис.1 представлена Таблица простых чисел до 1000.
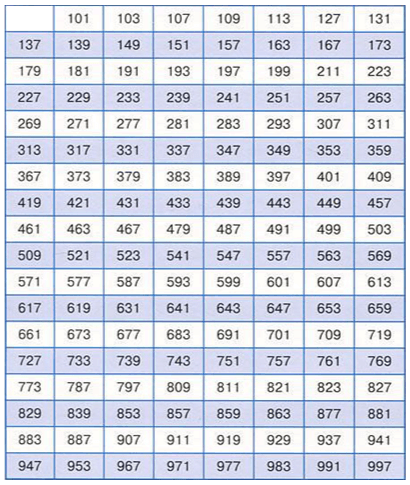
Представить таблицу для всех существующих простых чисел не является возможным. Поэтому, когда числовой ряд достигает 10000 или 1000000000, следует использовать решето Эратосфена.
Самое время будет рассмотреть Теорему 1 и Теорему 2, которые объяснят последнее утверждение.
Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.
Для данной теоремы можно привести следующее доказательство. Допустим, что в – это отличный от единицы наименьший делитель для числа с. Необходимо привести доказательство, используя методику противного, что является простым числом.
Допустим, что является натуральным составным числом. Отсюда следует, что для натурального числа в есть простой делитель составного числа, который отличен как от в, так и от единицы. Данный делитель можно обозначить в1. Далее, требуется, чтобы выполнялось условие 1 < в1 < в.
Из условия следует, что с делится на в, а в делится на в1. Понятие делимости можно выразить следующим образом с = в ⋅ q и в = в 1 ⋅ q 1 , откуда с = в 1 ⋅ ( q 1 ⋅ q), где q и q1 – это целые числа. Учитывая правило умножения целых чисел следует, что их произведение – это целое число с равенством с = в 1 ⋅ (q 1 ⋅ q). Из равенства видно, что в 1 выступает делителем для числа с. Следовательно, получаем несоответствие неравенства 1 <в 1 < в , поскольку в – это положительный наименьший и отличный от 1 делитель с.
Простых чисел бесконечно много.
В качестве доказательства можно взять предположительное конечное количество натурального числа m, обозначив, как m1, m2,…….., mn. Далее, необходимо рассмотреть вариант нахождения простого числа, которое будет отлично от указанных.
На рассмотрение можно взять число m, которое равно m1, m2,………, mn + 1. Оно не будет равно любому из чисел, которые соответствуют простым натуральным числам m1, m2,……, mn. Число m – простое. Так, можно считать, что теорема доказана. Если число m будет относиться к натуральным составным числам, тогда обозначение должно принять вид mn+1 и должно быть показано несовпадение делителя с m1, m2,……, mn.
Если бы утверждение не соответствовало этому, то с учетом свойств делимости произведения m1, m2,……, mn, получалось бы, что оно делится на mn+1. Так, второе слагаемое данной суммы, равное 1, требовалось бы делить на выражение mn+1, что является невозможным.
Среди любого заданного количества простых чисел может быть найдено любое простое число. Из данного утверждения следует вывод, что простых чисел представлено бесконечное множество.
Математика Эратосфена. Простые и составные числа
Решето Эратосфена — это специальный алгоритм, который позволяет определять все простые числа до целого заданного натурального числа N. Само название методики содержит основной принцип ее функционирования. «Решето» представляет собой «фильтр», пропускающий все ненужные числа, кроме простых.
Так, при составлении «решета» – таблицы, необходимо учитывать, что для выполнения задачи важна проверка чисел в последовательном порядке – начиная с двух и до 100, 1000 и т.д. Если у числа невозможно разложить на простые множители и делители отсутствуют – оно фиксируется в таблице, а если оно является натуральным составным числом, значит необходимо его исключить.
Составляя таблицу простых чисел в привычном порядке приходится поэтапно рассматривать каждую цифру. Необходимо начать с 2 – у нее можно выделить два делителя (1 и 2), поэтому оно является простым числом и может быть занесено в таблицу. Число 2, также, заносим в таблицу. Число 4 можно разложить на простые множители 2 и 2, а значит, в таблице его быть не должно, поскольку оно является составным. А 5 имеет всего два делителя, соответственно, оно фиксируется в таблице. Так, поочередно рассматривается каждое число, вплоть до 100, 1000, 10000 и т, д.
Данная методика является понятной, но весьма долгой и неудобной. Именно решето Эратосфена принято считать оптимальным алгоритмом. Далее, на примере приведенных таблиц будет рассмотрен сам алгоритм.
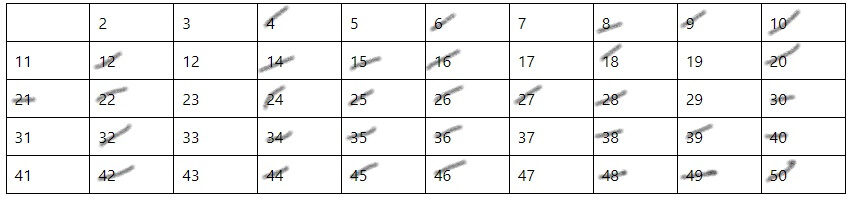
Найдем все простые натуральные числа от 2 до 50. Для начала, в таблицу заносятся все числа, которые располагаются в указанном числовом ряду
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 11 | 12 | 12 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
Далее выполняется последовательное зачеркивание всех чисел, кратных 2 (Рис.3).
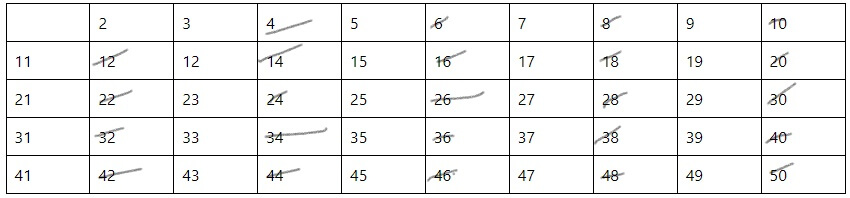
Затем, необходимо поочередно вычеркнуть все числа, кратные 3 (Рис. 4).
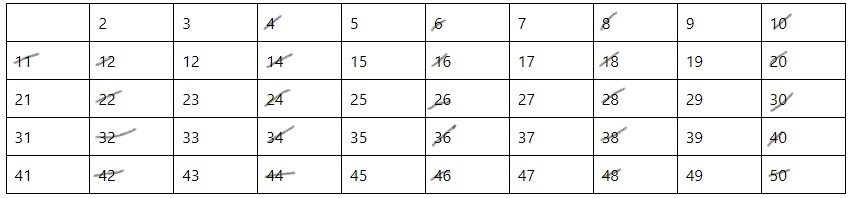
Также, необходимо поступить с числами, которые кратны 5 (Рис. 5).
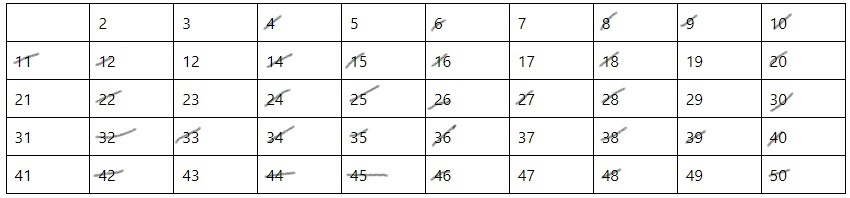
На последнем этапе зачеркиваются числа, кратные 7 и 11 (Рис. 6). В итоге будет получена окончательная таблица натуральных простых чисел от 2 до 50.
Далее стоит остановиться на формулировке Теоремы 3 и ее доказательстве.
Наименьший положительный и отличный от 1 делитель основного числа a
не превосходит √a, где √a арифметическим корнем заданного числа.
Необходимо обозначить b наименьший делитель составного числа a. Существует такое целое число q, где a=b·q, причем имеем, что b≤q. Недопустимо неравенство вида b>q, так как происходит нарушение условия. Обе части неравенства b≤q следует умножить на любое положительное число b, не равное 1. Получаем, что b·b≤b·q, где b2≤a и b≤√a
Доказанная теорема показывает, что при поочередном вычеркивании чисел из таблицы, необходимо начинать с числа, которое будет равно b² и должно соответствовать неравенству b² ≤ a. Если вычеркивание начнется с чисел, кратных 2, то в первую очередь будет вычеркнуто число 4, а если с кратных 3, то – число 9.
Используя методику Эратосфена при составлении простой числовой таблицы, можно обнаружить, что в процессе вычеркивания натуральных составных чисел, останутся лишь те простые числа, которые не будут превосходить значение квадратного корня из n.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Какие числа простые, а какие составные: примеры
Чтобы выяснить, какие числа простые, а какие составные, оптимальным решением станет использование признаков делимости. Более подробно можно рассмотреть это на Примере 1:
Пример 1
Необходимо доказать, что число 696969696969696969 является составным.
Решение
Сумма цифр данного числа будет равняться 9 ⋅ 6 + 9 ⋅ 9 = 9 ⋅ 15. Из этого следует, что для числа 9 ⋅ 15, 9 и 15 будут являться простыми делителями составного числа. Соответственно, число является составным и имеет как минимум три делителя.
Но, если необходима будет проверка, то следует использовать другие действия. Оптимальным способом станет числовой перебор. В процессе могут быть найдены составные и простые числа, которые не должны превосходить квадратный корень из а. Число разлаживается на простые множители. Если данное условие будет выполнено, значит, его можно считать простым.















