Каноническое уравнение прямой на плоскости: теория, примеры, решение задач
Понятие канонического уравнения прямой
Чтобы разобраться, что такое каноническое уравнение, нужно рассмотреть следующий пример. Дана прямоугольная система координат, в которой задана некая произвольная прямая. Известны координаты произвольной точки на отрезке \[M_{1}\left(x_{1}, y_{1}\right)\] и координаты направляющего вектора \[\bar{a}=\left(a_{x^{\prime}} a_{y}\right)\]. Используя все имеющиеся данные составим и запишем уравнение, которое будет описывать данную заданную прямую.
Рассмотрим точку \[\mathrm{M}(x, y)\]. Вектор \[\overline{M_{1} M}\] можно отнести к направляющим исходной линии в координатной плоскости. Координатами вектора будут точки \[\left(x-x_{1}, y-y_{1}\right)\]. Чтобы правильно определить векторные координаты, необходимо вспомнить основное правило решения векторов.
Произвольные точки \[M(x, y)\] будут являться основой для необходимой прямой с направляющим вектором \[\bar{a}=\left(a_{x}, a_{y}\right)\], только тогда, когда вектора \[\overline{M_{1} M}\] и \[\bar{a}=\left(a_{x}, a_{y}\right)\] будут являться коллинеарными по отношению друг к другу.
Исходя из этого можно составить формулу коллинеарности двух векторов.
\[\overline{M_{1} M}=\lambda \cdot \overline{\mathrm{a}}, \lambda \in R\]
Где:
После преобразования данного равенства в координатную форму, можно получить следующее уравнение:
Однако, обязательно выполнение главных условий: \[a_{x} \neq 0\] и \[a_{y} \neq 0\].
При выполнении вышеперечисленных условий, получаем следующие равенства:
Все выполненные преобразования привели к тому, что мы получили окончательную формулу канонического уравнения на плоскости \[\frac{x-x_{1}}{a_{x}}=\frac{y-y_{1}}{a_{y}}\].
Иначе такое равенство, еще называют уравнением прямой канонического вида.
Используя данную запись \[\frac{x-x_{1}}{a_{x}}=\frac{y-y_{1}}{a_{y}}\], можно в прямоугольной системе координат задать прямую, которой будет характерен направляющий вектор \[\bar{a}=\left(a_{x}, a_{y}\right)\]. Также данная линия будет проходить через заданную точку \[M_{1}\left(x_{1}, y_{1}\right)\].
Например: задано уравнение \[\frac{x-2}{\sqrt{3}}=\frac{y-3}{1}\]. Задается линия, которая будет проходить через точки \[M_{1}(2,3)\]. Ее направляющий вектор имеет координатные точки: \[\bar{a}=(\sqrt{3}, 1)\].
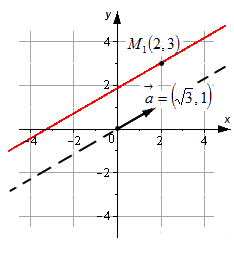
Когда любая прямая в системе координат проходит через две любые точки \[M_{1}\left(x_{1}, y_{1}\right)\] и \[M_{2}\left(x_{2}, y_{2}\right)\] и имеет направляющий вектор \[\bar{a}=\left(a_{x}, a_{y}\right)\], множество всех векторов можно записать как \[\mu \cdot \overline{\mathrm{a}}=\left(\mu \cdot \mathrm{a}{x^{\prime}} \mu \cdot a{y}\right), \mu \in R, \mu \neq 0\].
Таким образом, каждое уравнение прямой канонического вида \[\frac{x-x_{1}}{a_{x}}=\frac{y-y_{1}}{a_{y}}\], будет соответствовать заданной прямой на плоскости.
В системе координат задана прямая, которая проходит через точки \[M_{1}(2,4)\], и имеет направляющий вектор \[\bar{a}=(1,-3)\].
Решение задачи:
Составим и запишем общий вид канонического уравнения \[\frac{x-x_{1}}{a_{x}}=\frac{y-y_{1}}{a_{y}}\].
Далее подставим в него заданные значения \[x_{1}=2, y_{1}=-4, a_{x}=1, a_{y}=-3\].
Проведем необходимый расчет и получим следующую запись:
\[\frac{x-x_{1}}{a_{x}}=\frac{y-y_{1}}{a_{y}} \Leftrightarrow \frac{x-2}{1}=\frac{y-(-4)}{-2} \Leftrightarrow \frac{x-2}{1}=\frac{y+4}{-3}\].
Ответ: \[\frac{x-2}{1}=\frac{y+4}{-3}\]
Каноническое уравнение на плоскости с точками ax и ay равными нулевому значению
При условии, что одно из значений переменной является нулю, будет использоваться первоначальный вид уравнения. Две переменные нулевыми быть не могут, так как это невозможно по определению. Направляющий вектор не может быть нулевым.
В такой ситуации выражение \[\frac{x-x_{1}}{a_{x}}=\frac{y-y_{1}}{a_{y}}\] считается условным, и его нужно понимать как равенство \[a_{y}\left(x-x_{1}\right)=a_{x}\left(y-y_{1}\right)\].
Если \[\frac{x-x_{1}}{0}=\frac{y-y_{1}}{a_{y}}\] при \[a_{x}=0\], а заданная прямая проходит через точки \[M_{1}\left(x_{1}, y_{1}\right)\]. В данном случае она является параллельной относительно оси ординат. Если \[x_{1}=0\], то прямая будет совпадать с осью координат.
Утверждение необходимо доказать. Для заданной прямой вектор \[\bar{a}=\left(a_{x}, a_{y}\right)\] является направляющим. Также данный вектор будет являться коллинеарным по отношению к координатному вектору \[\bar{j}=(0.1)\].
Если второй параметр является нулевым значением, то \[a_{y}=0\] и мы получим равенство \[\frac{x-x_{1}}{a_{x}}=\frac{y-y_{1}}{0}\]. Данное уравнение характеризует прямую, которая проходит через точку \[M_{1}\left(x_{1}, y_{1}\right)\] и располагается параллельно оси абсцисс. Это утверждение будет правдивым, так как \[\bar{a}=\left(a_{x^{\prime}} 0\right)\], и является для прямой направляющим вектором. А вектор, в свою очередь, коллинеарен по отношению к вектору координат \[\bar{j}=(0.1)\].
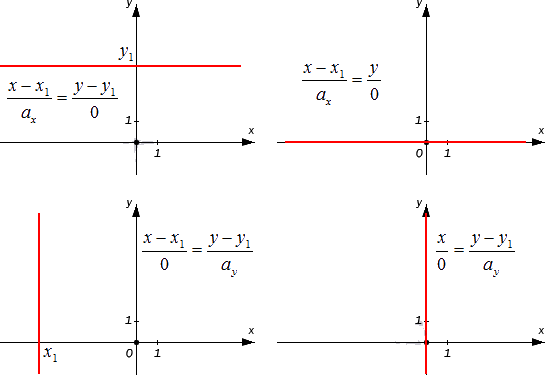
На координатной плоскости задана прямая, которая расположена параллельно оси Oy. Она проходит через точку
\[M_{1}\left(\sqrt[3]{2},-\frac{1}{7}\right)\].
Необходимо составить каноническое уравнение для заданной прямой, используя исходные данные.
Решение:
Так как прямая по отношению к координатной оси является параллельной, можно использовать координатный вектор
\[\bar{j}=(0.1)\]. Данный вектор будет служить, как направляющий.
Искомое уравнение будет выглядеть в следующем виде:
\[\frac{x-\sqrt[3]{2}}{0}=\frac{y-\left(-\frac{1}{7}\right)}{1} \Leftrightarrow
\frac{x-\sqrt[3]{2}}{0}=\frac{y+\frac{1}{7}}{1}\].
Ответ: \[\frac{x-\sqrt[3]{2}}{0}=\frac{y+\frac{1}{7}}{1}\].
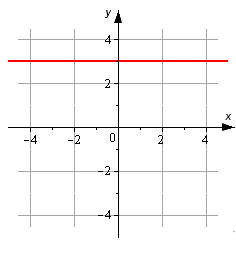
Согласно графику, нужно составить каноническое уравнение прямой.
Решение:
Исходя из графика можно сказать, что линия параллельна оси Ox и проходит через точку \[M_{1}(0,3)\].
Используем координатный вектор как направляющий.
Записываем каноническое уравнение: \[\frac{x-0}{1}=\frac{y-3}{0} \Leftrightarrow
\frac{x}{1}=\frac{y-3}{0}\].
Ответ: \[\frac{x}{1}=\frac{y-3}{0}\].
Преобразование канонического уравнения прямой в уравнение другого вида
Стандартную форму канонического уравнения \[\frac{x-x_{1}}{a_{x}}=\frac{y-y_{1}}{a_{y}}\] можно поставить в систему параметрических уравнений для плоскости.
Для преобразования одного вида уравнения в другой необходимо одну часть уравнения приравнять к другой.
Задана прямая на плоскости в виде канонического уравнения \[\frac{x+2}{3}=\frac{y-1}{11}\].
Необходимо записать параметрическое уравнение для прямой.
Принцип решения задачи:
Нужно поставить знак равенства между отдельными частями уравнения и переменной \[\lambda\]. Получается
следующий вид уравнения: \[\frac{x+2}{3}=\lambda\] и \[\frac{y-1}{11}=\lambda\].
Далее можно записать необходимы уравнения параметрического вида:
\[\frac{x+2}{3}=\lambda\] и \[\frac{y-1}{11}=\lambda.\].
\[\Leftrightarrow x+2=3 \cdot \lambda\] и
\[y-1=11 \cdot \lambda \Leftrightarrow x=-2+3 \cdot \lambda\] и \[y=1+11 \cdot \lambda\]
Ответ: \[x=-2+3 \cdot \lambda\] и \[y=1+11 \cdot \lambda\].
Задана на плоскости прямая при помощи канонического уравнения \[\frac{x-1}{2}=\frac{y+4}{0}\].
Необходимо составить общей вид канонического уравнения для данной прямой.
Решение:
Аналогичным образом решаем задачу, как в предыдущем примере:
\[\frac{x-1}{2}=\lambda\] и \[\frac{y+4}{0}=\lambda\].
\[\Leftrightarrow x-1=2 \cdot \lambda\] и \[y+4=0
\cdot \lambda \Leftrightarrow x=-2+1 \cdot \lambda\] и \[y=-4+0 \cdot \lambda\]
\[\Leftrightarrow 0
\cdot(x-1)=2 \cdot(y+4) \Leftrightarrow y+4=0\]
Ответ: \[y+4=0\].

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Принцип решения задач на составление канонических уравнений
Первым делом канонические уравнения применяется для тех задач, где необходимо вычислить принадлежность точки к заданному отрезку на плоскости.
Рассмотрим несколько вариантов задач, и подробно опишем их решение.
Задана линия, каноническое уравнение которой выглядит следующим образом:
\[\frac{x-1}{2}=\frac{y+\frac{1}{2}}{-3}\].
Нужно определить принадлежат ли две точки \[M_{1}\left(3,-3 \frac{1}{2}\right)\] и \[M_{2}(5,-4)\]
прямой.
Решение:
Для того чтобы проверить принадлежность прямой, нужно подставить заданные координаты точек в каноническое
уравнение.
Выполнив данное действие получим верное равенство: \[\frac{3-1}{2}=\frac{-3 \frac{1}{2}+\frac{1}{2}}{-2}
\Leftrightarrow 1=1\].
Согласно результату, можно сказать что точка \[M_{1}\left(3,-3 \frac{1}{2}\right)\] принадлежит заданному
отрезку.
Аналогичным образом нужно поступить и с другой точкой.
\[\frac{5-1}{2}=\frac{-4 \frac{1}{2}+\frac{1}{2}}{-3} \Leftrightarrow 2=\frac{7}{6}\]
Полученное в ходе решения равенство не является верным, следовательно, точка \[M_{2}(5,-4)\] не будет ей
принадлежать.
Ответ: прямой принадлежат координаты точки \[M_{1}\left(3,-3 \frac{1}{2}\right)\], координаты точки
\[M_{2}(5,-4)\] нет.
Заданы координаты двух точек \[M_{1}(2,4)\] и \[M_{2}(-1,3)\]. Нужно определить, будет ли заданная прямая на
плоскости с помощью уравнения \[\frac{x-2}{0}=\frac{y-3}{2}\], проходить через заданные координаты.
Решение:
Уравнение \[\frac{x-2}{0}=\frac{y-3}{2}\] можно преобразовать, и записать как \[2 \cdot(x-2)=0 \cdot(y-3)
\Leftrightarrow x-2=0\].
Заданные координаты точек подставим преобразованное уравнение, и произведем проверку.
Для точки \[M_{1}(2,4) 2-2=0 \Leftrightarrow 0=0\].
Так как равенство верное, можно сделать вывод, что точка принадлежит прямой.
Аналогичным образом проводится проверка второй точки: \[M_{2}(-1,3)\]
\[-1-2=0 \Leftrightarrow-3=0\].
Равенство неверное, поэтому точка \[M_{2}(-1,3)\] не принадлежит прямой.
Ответ: через точку \[M_{1}(2,4)\] прямая будет проходить, так как равенство верное, через точку
\[M_{2}(-1,3)\] нет.
Задачи, в которых заданы точки с координатами, будут являться наиболее простыми по отношению нахождения
канонического уравнения прямой.
Наиболее сложнее решаются задачи, когда предварительно необходимо определить координаты точек, через которые
проходит прямая.
Наиболее распространенной является тип задач, где нужно доказать прохождение прямой, через заданные точки.
Задана прямая, которая проходит через точки \[M_{1}(0,-3)\] и \[M_{2}(2,-2)\] в прямоугольной системе координат. Согласно условию задачи, необходимо составить каноническое уравнение.
Решение:
Вычислим координаты вектора \[\overline{M_{1} M_{2}}=(2.1)\], по уже известной методике решения, используя заданные точки. По отношению к прямой данный вектор будет направляющим.
\[\frac{x-0}{2}=\frac{y-(-3)}{1} \Leftrightarrow \frac{x}{2}=\frac{y+3}{1}\]
Ответ: \[\frac{x-0}{2}=\frac{y-(-3)}{1} \Leftrightarrow \frac{x}{2}=\frac{y+3}{1}\].















