Системы уравнений с двумя переменными, способы решения
Понятие системы уравнений с двумя переменными
Уравнениями называются математические равенства разной степени сложности, в которых одна или несколько величин неизвестны. Значения всех переменных нужно найти таким образом, чтобы в результате их постановки в первоначальное уравнение получилось верное числовое равенство.
Под системой уравнений понимается условие, которое заключается в одновременном выполнении нескольких уравнений, логически связанных между собой, относительно одной или нескольких переменных. Рассмотрим все варианты решения систему уравнений с двумя переменными.
Основные виды систем уравнений
В математике насчитывается достаточно много видов систем уравнений. Для более удобного их изучения и нахождения решений их разделяют на несколько групп с определёнными характеристиками.
Классификация помогает рассматривать системы уравнений разных видов. Первый вариант – это классифицирование по количеству уравнений в системе. Если оно всего одно, то его называют обычным уравнением. Если уравнений несколько, тогда речь идет о системе.
Отличительным критерием для другого вида классификации является количество переменных. Если переменная одна, значит это уравнение с одной неизвестной, если их две – то с двумя неизвестными и т.д.
Основные способы решения системы уравнений
Для того чтобы решить систему уравнений с двумя переменными, необходимо определить значения пары переменных, которые при подстановке в каждое из уравнений обратят их в верные числовые неравенства. Если удалось вычислить эти значения правильно, то они и будут являться решением для всех уравнений рассматриваемой системы.
В алгебре некоторые системы уравнений могут вовсе не иметь правильных решений или наоборот их может быть бесконечное множество. Убедиться в этом можно, если заняться углубленным изучением данной тематики. В итоге можно прийти к выводу, что системы представляют собой множества решений всех ее уравнений.
Рассмотрим основные способы решения систем с двумя неизвестными:
- способ подстановки;
- графический способ;
- способ сложения;
- способ введения новых переменных.
Чтобы подробно описать принцип решения на примере первых трех способов, будем рассматривать системы линейных уравнений с двумя неизвестными.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Способ подстановки
Этот способ считается одним из самых понятных и часто используемых для быстрого нахождения решения. Он заключается в следующем:
- в любом уравнении системы y выражается через x;
- полученное выражение подставляется в другое уравнение в результате чего остается только одна неизвестная;
- после решения уравнения определяется значение x;
- после этого легко вычисляется переменная y.
\[\left\{\begin{array}{c}3 x+2 y=16 \\2 x-y=6\end{array}\right.\]
Для того чтобы решить систему, выразим y через x во втором уравнении.
\[y=2 x-6\]
Подставим полученное выражение в первое уравнение и найдем значение x.
\[\begin{aligned}&3 x+4 x-12=16 \\&7 x=28 \\&x=4\end{aligned}\]
После этого найдем значение y.
\[y=8-6=2\]
Ответ (4,2).
Способ сложения
Алгоритм решения системы линейных уравнений с двумя переменными заключается в выполнении последовательных действий:
- сначала нужно уравнять модули коэффициентов при одном неизвестном;
- сложить либо вычесть уравнения системы;
- решить объединенное уравнение и найти значение одной переменной;
- вычислить второе неизвестное.
Рассмотрим решение с помощью этого способа на том же примере.
\[\left\{\begin{array}{c}3 x+2 y=16 \\2 x-y=6\end{array}\right.\]
Умножим второе уравнение на 2, в результате получим:
\[\left\{\begin{array}{l}3 x+2 y=16 \\4 x-2 y=12\end{array}\right.\]
Теперь произведем сложение этих уравнений
\[\begin{aligned}&3 x+2 y+4 x-2 y=16+12 \\&7 x=28 \\&x=4\end{aligned}\]
Теперь можно определить значение y из второго уравнения.
\[\begin{aligned}&y=8-6 \\&y=2\end{aligned}\]
Ответ (4,2).
Способ введения переменных
Этот способ позволяет упростить исходную систему квадратных уравнений для последующего решения в линейном виде.
Этот способ рассмотрим на примере следующей системы квадратных уравнений:
\[\left\{\begin{array}{c}3^{x}+2^{y+1}=35 \\2^{y}+3^{x}=31\end{array}\right.\]
Решение:
Данная система линейных уравнений равносильна следующей системе:
\[\left\{\begin{array}{c}3^{x}+2 * 2^{y}=35 \\2^{y}+3^{x}=31\end{array}\right.\]
Пусть \[3^{x}=u(u>0), \text { a } 2^{y}=v(v>0)\], получим:
\[\left\{\begin{array}{c}u+2 v=35 \\u+v=31\end{array}\right.\]
Далее полученную систему решим с помощью метода сложения, находим:
\[\begin{aligned}&u+2 v-u-v=35-31 \\&v=4 \\&u=31-4=27\end{aligned}\]
Возвращаемся опять к замене и получим новую систему:
\[\begin{gathered}3^{X}=27 \\2^{y}=4\end{gathered}\]
Получаем далее:
\[\left\{\begin{array}{l}x=3 \\y=2\end{array}\right.\]
Ответ: (3,2).
Графический способ
Наиболее наглядным является графический способ решения систем уравнений. Он заключается в том, что на координатной плоскости изображаются оба уравнения и в итоге находится точка пересечения графиков. Ее координаты и будут соответствовать значениям переменных.
В обоих уравнениях выразим y через x, получим:
Изобразим графики на координатной плоскости:
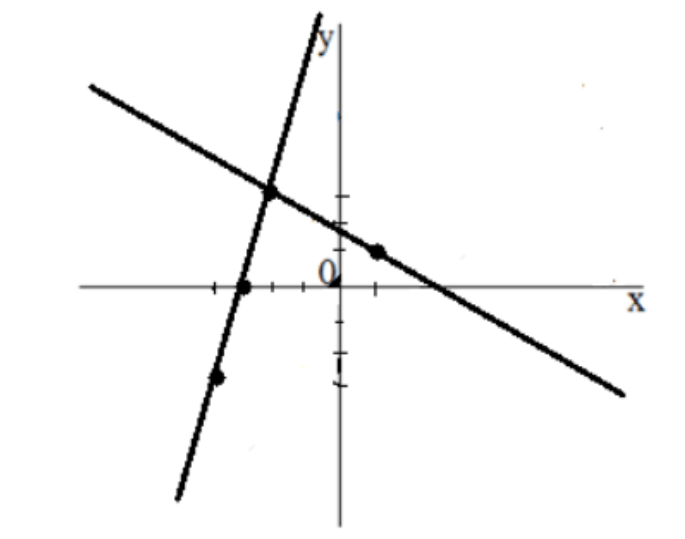
Ответ: (−2, 3).















