Свойства арифметических корней и их характеристики
Данный материал включает в себя всю информацию связанную с понятием квадратный корень числа.
Мы подробно изучим все основные свойства корней. Когда применяются корни чисел, как правильно работать с этим элементом алгебры. Закрепим изученный материал на конкретных примерах решения задач.
Для начала дадим определение понятию корень.
Квадратный корень — это такое число, которое во второй степени равно подкоренному выражению.
Принцип вычисления корня: все значения, которые находятся под корнем, называют подкоренным выражением. Оно может быть выражено, как числом, так и буквой. Числовых значений под корнем может быть несколько, это также допускается.
Свойства арифметического квадратного корня
Нужно обязательно помнить: извлекать корень можно только из положительного числа.

Квадратный корень из нуля, всегда равняется нулевому значению.
Как правильно определить корень из любого числа?
Для облегчения задачи достаточно знать и выучить таблицу корней. Она очень существенно помогает в данной ситуации.
Примеры решения задач с определением квадратного корня числа:
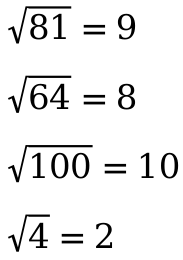
Вычисление значения корня из десятичной дроби:
- преобразовать число из десятичной дроби в целое число, убрав запятые;
- найти квадратный корень для полученного целого действительного числа;
- полученное целое действительное значение, заменить на дробь десятичного значения, применяя правило перемножения дробей.
Пример №1:
Нужно определить квадратный корень из следующего значения \[\sqrt{0,16}\]
Для начала убираем запятую из дробного выражения и получаем число равным 16.
Квадратичное значение из шестнадцати равняется четырем.
Применяем правило перемножения дробей десятичного значения.
В результате проведенных вычислений, количество знаков, после запятой равно сумме знаков.
Если мы перемножим 0,16 * 0,3 = 0,048. Видим, что в ответе на этот пример, три знака после запятой. Общая сумма знаков до запятой.
Затем нам нужно преобразовать заданное значение до десятичной дроби, то есть один знак за запятой. Умножить дробь на саму себя и получаем ответ. В котором два знака за запятой.
Получаем ответ задачи: 0,4.
Следовательно: \[\sqrt{0,16}=0,4 \text { или } 0,4^{2}=0,16\].
Пример №2:
Нужно определить квадратный корень из следующего значения \[\sqrt{0,81}\]
Для начала убираем запятую из дробного выражения и получаем число равным 81.
Квадратичное значение из шестнадцати равняется четырем.
Применяем правило перемножения дробей десятичного значения.
В результате проведенных вычислений, количество знаков, после запятой равно сумме знаков.
Если мы перемножим 0,14 * 0,3 = 0,042. Видим, что в ответе на этот пример, три знака после запятой. Общая сумма знаков до запятой.
Затем нам нужно преобразовать заданное значение до десятичной дроби, то есть один знак за запятой. Умножить дробь на саму себя и получаем ответ. В котором два знака за запятой.
Получаем ответ задачи: 0,4.
Следовательно: \[\sqrt{0,81}=0,9 \text { или } 0,9^{2}=0,81\].
Рассмотрим основные свойства корней числовых значений:
- Перемножение действительных чисел.
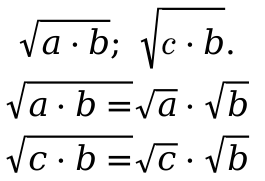
Данное свойство можно расписать в виде множества чисел:
- Вычисление корня числа из частного значения множества действительных чисел.
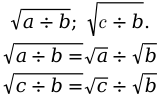
Можно записать данное деление и другим способом:
Условие: \[a \geq 0 ; b>0\].
Значение в знаменателе обязательно должно, быть более нуля, так как по законам математики делить н ноль нельзя.
- Свойство с четным показателем, действительного числа.
\[\sqrt{a^{2 m}}\]. Значение a — может быть любым.
Всем трем свойствам характерна смена частей множества местами. Например, рассмотрим деление значений:
Первое и второе свойство можно доказать, опираясь на определение корня квадрата и основных свойств степеней, с натуральным показателем.
Для доказательства третьего свойства, применяется понятие как модуль числа.
Свойство квадратного корня и степени
Принцип доказательства при помощи квадратного корня. Все действительные числа должны быть положительные или равные нулю.
Запишем равенство: \[(\sqrt{a} \cdot \sqrt{b})^{2}=(\sqrt{a})^{2} \cdot(\sqrt{b})^{2}\].
Следовательно: \[(\sqrt{a})^{2}=a,(\sqrt{b})^{2}=b\].
Таким же образом, поступим при доказательстве множества числа.
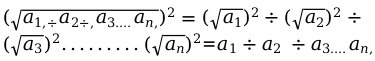
Из этого следует следующее равенство: \[\sqrt{a_{1,+} a_{2+}, a_{3 \ldots} a_{n_{1}}}=\sqrt{a_{1}} \div \sqrt{a_{2}} \div \sqrt{a_{3}} \ldots \ldots \ldots \sqrt{a_{n}}\].
Примеры решения:
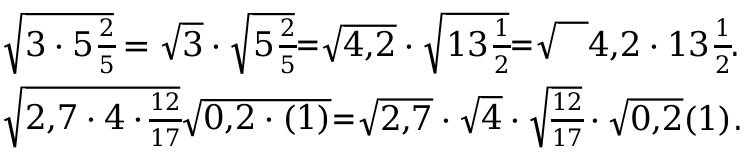
Докажем основное свойство квадратного корня частного:
Записываем равенство значений.
При этом \[\sqrt{a} \text { и } \sqrt{b}\] — являются положительными значениями и соответственно равные нулю.
Рассмотрим случай нахождения квадрата из корня.
Чтобы доказать данное свойство, \[\sqrt{a^{2}}\]необходимо рассмотреть следующее неравенство.
При \[a \geq 0, \sqrt{a^{2}}=a\].
Если составить неравенство a < 0 будет соответствовать следующее равенство \[\sqrt{a^{2}}=-a\].
Пример №1:
Пример №2:

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Свойство корня n-ой степени
Для степенного корня, характерно множество основных характеристик.
Мы рассмотрим их все подробно и разберем доказательство каждого свойства на примерах.
Пример 1: Свойство, состоящее из произведения нескольких значений. Они должны быть либо положительными по значению, либо равняться нулю. Выражать могут с помощью соответствующего равенства.
Это свойство применяется, чтобы выразить произведение чисел.
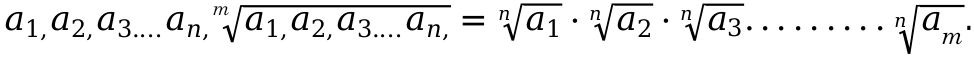
Далее докажем данное свойство, применяя следующее равенство.
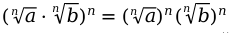
Руководствуясь определением корня, который находится в определенной степени, получим следующие равенства:
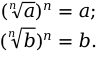
Итог: \[(\sqrt[n]{a} \cdot \sqrt[n]{b})^{n}=a \cdot b\].
Мы получили равенство, которое изначально нужно было доказать.
Доказать множество равенство значений, можно таким же методом, используя те же операции.
Рассмотрим несколько примеров решения функции данного вида, применяя числовые значения.
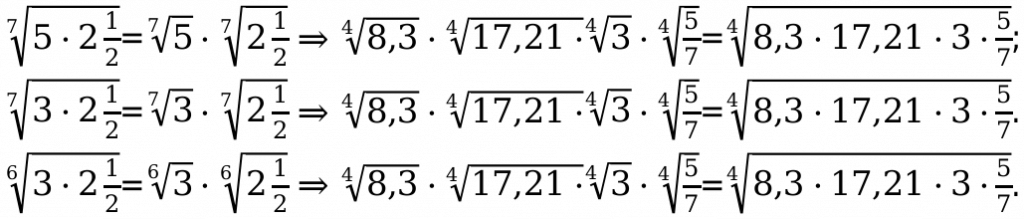
Пример 2: Дробное значение под корнем.
Числовое значение в числителе может иметь положительное значение или равняться нулю. В знаменателе — любое действительное число, кроме нуля. Так как по законам математики: деление на ноль запрещается (недопустимо).
Перейдем к доказательству свойства.
Запишем равенство \[\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}, \text { где } a \geq 0, b>0\]. (обязательное условие, которое должно соблюдаться).
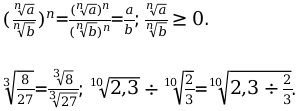
Пример 3: Это свойство заключается в следующем: если подкоренное число имеет любое значение и четный показатель. n = 2 * m;
Следовательно, справедливым будет равенство: \[\sqrt[2 \cdot m]{a^{2 \cdot m}}\].
Если показатель является нечетным значение, равенство запишется иначе, а именно: \[\mathrm{n}=2 \cdot m-1, \sqrt[2 \cdot m-1]{a^{2} \cdot m-1}\].
Докажем данное свойство.
Представим следующее равенство: \[\sqrt[2 \cdot m]{a^{2 \cdot m}}\] и \[\sqrt[2 \cdot m-1]{a^{2 \cdot m-1}}\] — для любых значений действительных чисел и натурального значения степени m. Когда \[a \geq 0\] справедливы считается равенство \[\sqrt[2 \cdot m]{a^{2 \cdot m}}\].
При \[a<0,-(a)^{2 m}=a^{2 m} \cdot \sqrt[2 m]{a^{2 \cdot m}=a}\] и \[\sqrt[2 \cdot m-1]{a^{2 \cdot m-1}}=a\], так как корень в нечетной степени можно расписать в виде выражения \[\sqrt[2 \cdot m-1]{-c}=-\sqrt[2 \cdot m-1]{c}\]. Где значение с — имеет положительное значение или равняется нулю. Для лучшего усвоения материала рассмотрим пример решения.
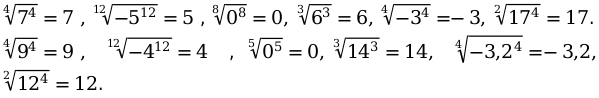
Пример 4: Извлечение действительного значения из-под корня.
Запишем следующую функцию \[\sqrt[n]{\sqrt[m]{a}}=\sqrt[n \cdot m]{a} \text { или } \sqrt[n 1]{\sqrt[n 2]{\ldots \ldots \sqrt[n k]{a}}}=\sqrt[n 1 \cdot n 2 \cdot n k]{a}\]
Значение числа a — может быть положительным значение либо равняться нулю, а показатель степени n и m обычные натуральные числовые значения.
Равенство \[\sqrt[n]{\sqrt[m]{a}}=\sqrt[n \cdot m]{a}\] докажем следующим способом.
Поменяем местами значения, которые расположены до знака равно и после него. Запишем новое уравнение \[\sqrt[n \cdot m]{a}=\sqrt[n]{\sqrt[m]{a}}\]. Далее вспомним как возводить степень в степень и основное определения корня числового значения. Используя их преобразуем следующее уравнение.
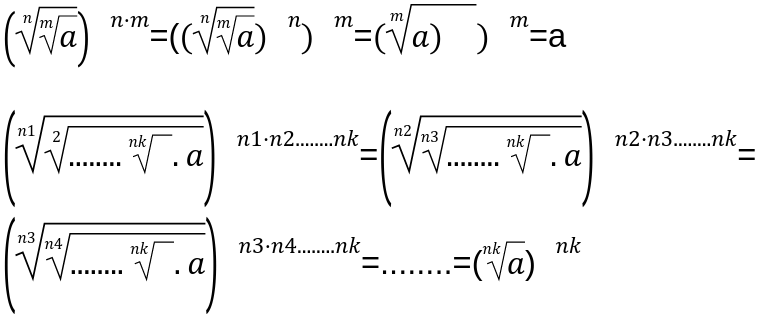
Разберем для более лучшего понятия на числовых примерах.
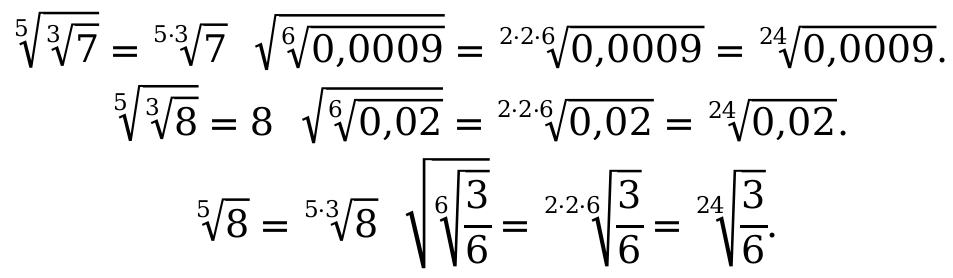
Пример 5: Числовое значение под корнем, является положительным, показатель степени любые натуральные числа.
Для начала докажем следующее выражение под корнем : \[\sqrt[n]{a}\].
Оно должно являться положительным значением или быть равным нулю. Когда происходит возведение степеней одна в одну, получаем am. Если изначально подкоренное значение положительное или нуль, то корень из этого числа также будет иметь значение со знаком плюс. \[\sqrt[n]{a^{n \cdot m}}=\left(\left(\sqrt[n]{a)}^{n}\right)^{m}\right.\]
Доказательство является справедливым. Например: \[\sqrt[12]{2^{3}}=4^{2}\].
Пример 6: Свойство степени из степени числового значения, имеющее положительное или нулевое значение, натуральную степень.
Запишем равенство числовых значений в виде уравнения.
Для этого докажем правдивость данного свойства корня из степени числа.
Степень является числом положительным, так как подкоренное значение больше или равно нулю.
Исходя из этого выражения доказательство считается верным.
Пример 7: Сравнительное свойство корней с одинаковыми показателями.
В данном свойстве наблюдаются следующие характеристики: значение a должно быть меньше значения b, a<b.
Необходимо доказать правдивость вышеупомянутого неравенства.
Для этого необходимо воспользоваться методом, который в алгебре носит название от противного. Записываем неравенство, но при этом меняем знак, на больше либо равно и получаем выражение: \[\sqrt[n]{a} \geq \sqrt[n]{b}\]
\[(\sqrt[n]{a})^{n} \geq(\sqrt[n]{b})^{n}\] из этого следует, что a>b, что не правдиво в отношении ранее изученного неравенства. Значит: \[\sqrt[n]{a}<\sqrt[n]{b}\] при a<b.
Пример 8: Сравнение, когда под корнем одинаковые числовые значения, а показатели, обязательно должны быть натуральными числами.
\[\sqrt[m]{a}>\sqrt[n]{a}\], при условии,что \[a>1 \quad \sqrt[m]{a}<\sqrt[n]{a}\].
Рассмотрим первую часть нашего неравенства. Первый показатель степени является больше, чем второй показатель. Подкоренное значение больше нуля, но меньше единичного значения \[\Rightarrow \sqrt[m]{a}>\sqrt[n]{a}\].
Если \[\sqrt[m]{a} \leq \sqrt[n]{a}\], при помощи свойства упростим данное неравенство и получим следующий вид:
Согласно свойству, у которого натуральный числовой показатель выполняется неравенство
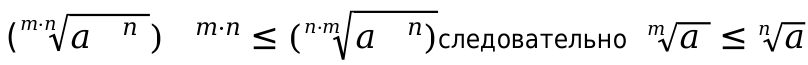
Пример 9:
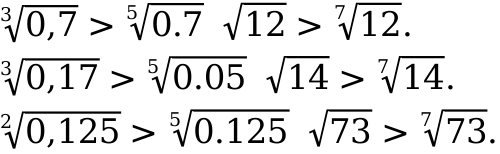
Калькулятор квадратных корней
Все изученные свойства арифметических корней имеют важную роль в математике. Применяя их, можно быстро преобразовать сложные на первый взгляд уравнения.















