Угол между прямой и плоскостью
Основное определение: «Угол, возникающий между перпендикулярными отрезками, опущенными в пределах этих плоскостей к линии пересечения и является углом между плоскостями».
Чтобы построить проекцию прямой на плоскость, достаточно опустить из любых двух ее точек перпендикуляры на плоскость (спроектировать эти точки), после чего провести через них прямую – это и будет проекция.
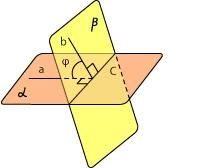
Виды углов между плоскостью
Плоскость и прямая имеют одну точку пересечения (общую).
В данном примере угол между прямой и плоскостью нам не известен. Прямая также может проходить через плоскость перпендикулярно (90 градусов)
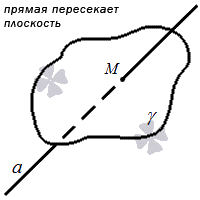
Прямая перпендикулярна плоскости, а также всем остальным прямым, расположенным на данной плоскости.
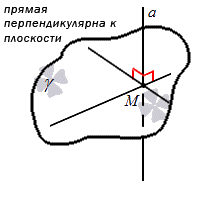
Точка перпендикулярного пересечения прямой М1 и плоскости γ под является одновременно и проекцией точки М, при условии, что она не принадлежит плоскости γ.
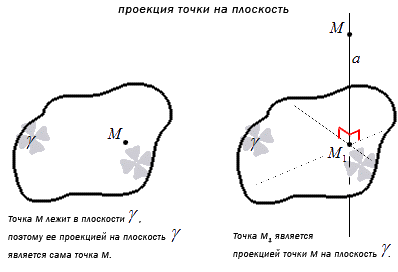
Проекция прямой на плоскость обозначает множество проекция данной прямой на плоскость.
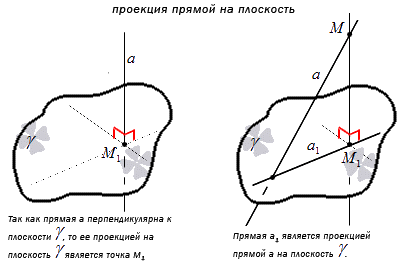
Это означает, что прямая, перпендикулярная к плоскости имеет с ней общую точку пересечения, из чего следует то, что a – принадлежит плоскости и проходящей через точку пересечения прямой плоскости.
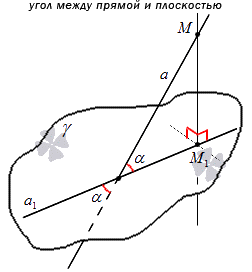
Углом между прямой и плоскостью является угол между данной прямой и ее проекцией на заданную плоскость.
Прямая необязательно перпендикулярна плоскости. Из этого обозначения следует, что угол между прямой и плоскостью всегда является острым (90>x).
Угол между прямой и плоскостью всегда равен 90 градусам, в то время как угол между параллельно расположенными прямыми определять не требуется. В некоторых заданиях, его значение просто приравнивается нулю, это указывают внутри задания.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Как найти угол между прямой и плоскостью
Способов решения задач на нахождения угла между плоскостью и заданной прямой, бесчисленное множество. Путь, которым необходимо решить задачу, выбирается исходя из указанных в условиях задачи данных. Зачастую, рельсами решения задач такого типа являются тангенсы, косинусы, синусы углов, а также признаки подобия/равенства фигур. Далее будет рассмотрен метод решения с применением сетки координат.
Геометрический метод. При геометрическом методе нужно найти какую-нибудь удобную точку на прямой, опустить перпендикуляр на плоскость, выяснить, что из себя представляет проекция, а потом решать планиметрическую задачу по поиску угла (φ) в треугольнике (зачастую прямоугольном).
Решение задачи геометрическим методом. Поскольку в правильной пирамиде высота опускается в центр основания O, то OE – это проекция SE, а точка M проецируется в точку K – середину отрезка OE.
И теперь FK – это проекция FM, а искомый угол между прямой FM и плоскостью основания – это ∠MFK.
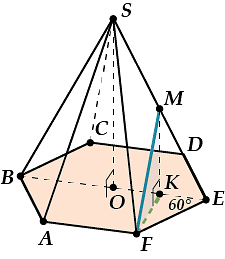
Ищем этот угол. Пусть стороны основания равны какому – то a, тогда боковые рёбра – 3a. Заметь, что ΔMFK – прямоугольный и в этом треугольнике нам нужно найти острый угол.
Алгебраический метод. При алгебраическом методе вводится система координат, определяются координаты двух точек на прямой и уравнение плоскости, а затем применяется формула вычисления угла между прямой и плоскостью.
Здесь \[\left(x_{1}, y_{1}, z_{1}\right),\left(x_{2}, y_{2}, z_{2}\right)\] — координаты двух точек на прямой, A, B, C- координаты в уравнении плоскости: \[ A x+B y+C z+D=0 \].
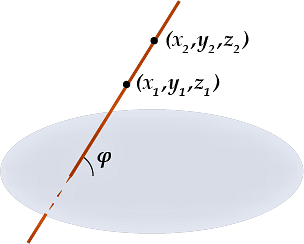
В 3D используется система координат, состоящая из трех направлений – Охуz.
В ней задается прямая, которая пересекается с заданной плоскостью в точке М. В данном примере требуется найти угол а, который находится между прямой и плоскостью.
Для нахождения угла а, возьмем уравнение прямой и вектор прямой пространства, а плоскости соответствует равенство плоскости и вектор плоскости. Из этого следует: → a = ( a x , a y , a z ).
\[\vec{a}=\left(a_{x}, a_{y}, a_{z}\right)\] — есть направляющий вектор данной прямой, в то время как → n ( n x , n y , n z ) является нормальным вектором для заданной плоскости. \[\vec{n}\left(n_{x}, n_{y}, n_{z}\right)\].
При помощи уравнения, в случае если в задании уже есть координаты направляющего вектора прямой и нормального вектора плоскости можно найти векторы а и n.
Имеющуюся у нас формулу моно преобразовать, что позволит получить требуемый угол, применяя координаты направляющего вектора прямой и нормального вектора.
Всего есть 4 возможных варианта расположения векторов а и n относительно данных прямых и плоскости. На рисунке ниже даны все 4 разновидности их расположения.
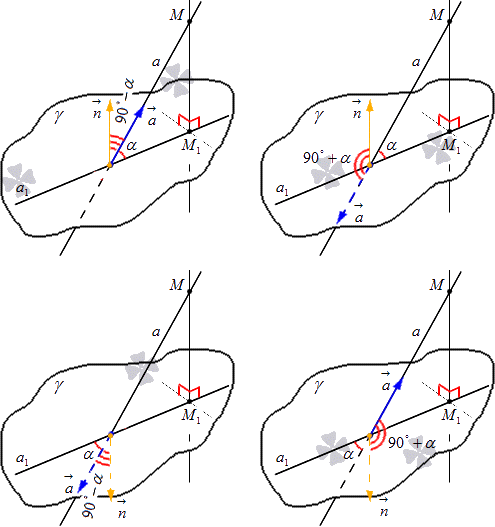
Угол между указанными векторами обозначается как ( ˆ→ a , → n ) \[\vec{a}=\left(a_{x}, a_{y}, a_{z}\right)\], являясь острым. Необходимый нам угол а дополняется. Теперь мы имеем выражение \[(\overbrace{{\vec{a}}, \vec{n}})=90^{\circ}-\alpha\].
Если по условию задачи \[(\overbrace{\vec{a}, \vec{n}})>90^{\circ}\] ( ˆ → a , → n ) > 90 °,то получается выражение ( ˆ → a , → n ) = 90 ° + α.
Также необходимо добавить. Что косинусы равных углов равны. Исходя из этого можно составить равенства:
При помощи формулы приведения можно упростить выражение. Получится:
После некоторых преобразований вырисовывается система:
Подведем итог: синус угла между плоскостью и прямой равняется модулю косинуса угла, расположенного между вектором прямой и нормальным вектором заданной плоскости.
Угол образованный двумя векторами имеет значение скалярного произведения векторов и этих длин. При помощи формулы, приведенной ниже, можно вычислить синус угла, полученного пересечением плоскости и прямой.
Все это можно привести к следующему виду:
Применив основное тригонометрическое свойство, возможно вычислить косинус, но только при условии. Что синус уже известен/дан в условии задания. Как было сказано выше, угол, образованный пересечением прямой и плоскости, является острым. Это означает, что значение этого угла всегда положительно. Его можно найти формулой \[\alpha=\sqrt{1-\sin \alpha}\].
Для более хорошего понимания материала, рассмотрим несколько примеров и попробуем их решить.
Пример 1:
Ha векторах \[\overrightarrow{A B}=(1,0,2), \quad \overrightarrow{A C}=(-1,3,0), \overrightarrow{A D}=(4,1,1)\] построена пирамида.
Найдите угол между прямой AD и плоскостью ABC .
Решение:
Чтобы вычислить угол между прямой и плоскостью по полученной формуле, нам нужно знать координаты направляющего вектора прямой и нормального вектора плоскости. Направляющим вектором прямой AD является вектор \[\overrightarrow{A D}=(4,1,1)\].
Нормальный вектор \[ \vec{n}\] плоскости ABC перпендикулярен и вектору \[\overrightarrow{A B}\] и вектору \[\overrightarrow{A C}\] , то есть, в качестве нормального вектора плоскости ABC можно взять векторное произведение векторов \[\overrightarrow{A B}\] и \[ \overrightarrow{A C}\]:
Осталось подставить координаты векторов в формулу и вычислить требуемый угол между прямой и плоскостью:
Ответ: \[\arcsin \frac{23}{21 \sqrt{2}}\]
Пример 2. Найти угол между прямой и плоскостью x-2 y+3 z+4=0.
Решение.
Из уравнения прямой найдем направляющий вектор прямой \[\bar{s}={2 ; 6 ;-3}\].
Из уравнения плоскости найдем вектор нормали плоскости \[\bar{q}={1 ;-2 ; 3}\].
Воспользовавшись формулой, найдем угол между прямой и плоскостью:
Ответ: \[\sin \varphi=\frac{19}{7 \sqrt{14}} \].
Дополнительные теоремы
- Углом между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется угол между прямой и ее проекцией на плоскость.
- Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
- Если прямая параллельна плоскости, то угол между ней и плоскостью М считается равным нулю. Если прямая перпендикулярна прямой, т.е. равен 90 градусам.
- Чтобы найти синус угла между прямой и плоскостью можно сначала вычислив косинус угла между прямой и перпендикуляром к плоскости.
- Если в пространстве заданы направляющий вектор прямой L s = {l; m; n} и уравнение плоскости Ax + By + Cz + D = 0, то угол между этой прямой и плоскостью можно найти, используя следующую формулу:















