Действия с дробями: правила, примеры

Главная
Справочник
Математика
Выражения
Действия с дробями: правила, примеры

Оглавление

Время чтения: 24 минуты

1 633

Действия с дробями общего вида
Алгоритм решения задач с обыкновенной дробью общего вида
Вычисление дробных значений с переменной
Вычислительные действия с десятичными дробями
Основные характеристики десятичных дробей
Принцип умножения десятичных дробей
Умножение десятичных дробей при помощи столбика
Умножение десятичной дроби с обыкновенной и со смешанной дробью
Возведение в степень дробного числового выражения
Преобразование дробных значений 0,1, 0,01, 0,001, где основанием степени является число 10
Правила деления дробей
Приведение дробей к наименьшему общему знаменателю
Решение задач с приведением к наименьшему знаменателю
Калькулятор вычисления НОД и НОК двух чисел

Действия с дробями общего вида

Для дробей общего вида характерно наличие числителя и знаменателя.

Значения которые, которыми выражены данные составляющие дроби, могут быть натуральными и числовыми выражениями.

Если рассмотреть подробно следующие дробные числа:

\[\frac{5}{4}, \frac{3,5}{5}, \frac{1+2,6}{4(6-1)}, \frac{\frac{3}{5}+\frac{7}{8}}{2,3-0,9}, \frac{1}{2 \sqrt{3}}\]

можно с уверенностью отметить, что и в числителе и знаменателе дробные выражения могут быть обозначены как:

десятичная дробь;
натуральный логарифм;
сумма и разность выражений;
дробь с постоянным значением числа.

Алгоритм решения задач с обыкновенной дробью общего вида

Когда необходимо произвести вычитание дробей с одинаковыми знаменателями, то в процессе решения суммируется только числитель дробей.
\[\frac{a}{b} \pm \frac{c}{b}=\frac{a \pm c}{b}\]
Где:
\[a, c, d_{0}\] и равные некоторым числовым значениям.
При выполнении сложения или вычитания дробей для различных значений в знаменателях, нужно выполнить приведение к общему знаменателю. Далее осуществить сложение или вычитание преобразованных дробей с одинаковыми числовыми значениями.
При перемножении дробных значений, выполняются следующие действия:
- произведение числителей;
- аналогичные действия , но только с знаменателями.
При выполнении деления, необходимо первую дробь перемножить на вторую, но в обратном значении. Иными словами произвести замену числителя на значение знаменателя.

Основные показатели и свойства дроби:

черта в дроби обозначает признак деления;
деление на числовое значение характеризуется как перемножение его на обратное значение;
возможность применения свойств, которые относятся для действительных чисел;
свойства для дробей и различного рода числовых неравенств.

Применяя данные свойства можно произвести преобразование дробных чисел:

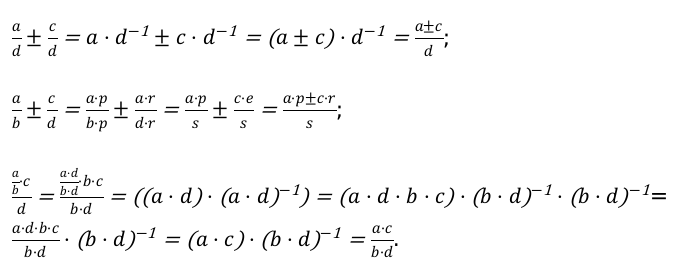
Пример №1:

Для заданных значений дроби: \[\frac{8}{2,7}\] и \[\frac{1}{2,7}\] необходимо выполнить сложение.

используя алгоритм решения, необходимо значения в числителе сложить, а в знаменателе оставить без изменений и переписать.

Выполнив все действия получим дробь: \[\frac{8+1}{2,7}\].

Далее произведем сложение и получим дробное значение:

\[\frac{8+1}{2,7}=\frac{9}{2,7}=\frac{90}{27}=3 \frac{1}{3}\]

Следовательно: \[\frac{8}{2,7}+\frac{1}{2,7}=\frac{8+1}{2,7}=\frac{9}{2,7}=\frac{90}{27}=3 \frac{1}{3}\]

Ответ задачи: \[\frac{8}{2,7}+\frac{1}{2,7}=3 \frac{1}{3}\].

Пример №2

Необходимо найти разность дробей:

\[\frac{1-\sqrt{2}}{3 \cdot\left(\log_{2} 3 \cdot \log_{2} 5+1\right)}\]

\[\frac{\sqrt[3]{2}}{3 \cdot\left(\log_{2} 3 \cdot \log_{2} 5+1\right)}\]

Так как в знаменателе данные являются равными между собой. вычисление будет производиться по принципу равного знаменателя.

Из этого следует:

\[\frac{1-\sqrt{2}}{3 \cdot\left(\log {2} 3 \cdot \log {2} 5+1\right)}-\frac{\sqrt[3]{2}}{3 \cdot\left(\log {2} 3 \cdot \log {2} 5+1\right)}=\frac{1-\sqrt{2} \sqrt{2}}{3 \cdot\left(\log {2} 3 \cdot \log {2} 5+1\right)}\]

Для решения данного типа задач важно помнить правило приведения к общему знаменателю.

Вычисление дробных значений с переменной

В случае, когда имеются одинаковые значения в знаменателях, то необходимо производить суммирование или вычитание числителей.

Дробь соответствующего вида можно упростить.

После проведения процесса упрощения дробного значения, окончательный вариант значения, если их несколько приводят к общему знаменателю.

Затем суммируют числитель и находят правильный ответ решения.

Вычислительные действия с десятичными дробями

В свою очередь данный вид дробей подразделяется на следующие категории:

Конечные — если после запятой присутствует окончательное число.
Например: \[\pm a_{0} a_{1} a_{2} a_{3} \ldots . . a_{n}\]
\[\pm \sum_{k=0}^{n} a_{k} \cdot 10^{-k}\]
Бесконечные — количество цифр после запятой, не имеют окончательного значения, то есть они бесконечны.
Например: \[\pm a_{0} a_{1} a_{2} a_{3}\]
\[\pm \sum_{k=0}^{n} a_{k} \cdot 10^{-k}\]

Основные свойства дробей:

Изменение величины десятичной дроби не произойдет, даже если к ней добавить справа несколько нулей. Это свойство принято считать одним из самых главных для данного вида дробей.

Если в рассматриваемом дробном значении наблюдается множество нулевых значений, тогда их просто исключают, так как никакого влияния на значение они не имеют.

Рассмотрим несколько простых и понятных для ознакомления примеров решения данных дробей

0,900 = 0,9;
22,10200000 = 22,102;
0,45000=0,45;
0,12569000=0,12569;
0,780=0,78.

Основные характеристики десятичных дробей

Дробное число, не будет иметь какого-либо значения, если в знаменателе нулевое число. Деление на ноль в математике строго запрещено.
Нулю будет равна дробь, у которой в числителе значится нулевое значение. В знаменатель — отсутствует.
Если значения, которые находятся в числителе и знаменателе разделить или перемножить на любое действительное число. То получится дробь равная ей по значении.
Если взять две дроби: \[\frac{a}{b}\] и \[\frac{c}{d}\] то они называться будут равными при \[a \cdot d \] или \[ b \cdot c .\]

Принцип умножения десятичных дробей

Для перемножения десятичных дробей необходимо, произвести следующие действия.

Дробь записать в виде так называемого математического столбика. Далее рассмотреть заданное значение, как обыкновенные действительные числа и подсчитать их;
Все знаки за запятой подсчитать и сложить сумму;
Полученную сумму справа налево отложить и поставить запятую.

Для данного вида дробей характерны все те же действия, что и для остальных чисел.

Если переставить местами множители, на окончательный ответ это не повлияет.

если мы хотим умножить число на произведение двух и более. Сначала перемножаем данное число на первый множитель затем полученное значение на второй и так далее.

Чтобы умножить сумму на множитель. Нужно по отдельности перемножить числа и полученную сумму сложить.

Если проводим умножение на разность чисел. Для начала умножаем на уменьшаемое, а затем на вычитаемое. Следовательно, полученные значения вычитаем.

Также процесс умножения можно упростить. Десятичные дроби перемножить как действительные целые числа, и поставить запятую.

Пример №1:

Определить произведение чисел \[1,5 \cdot 0,75\].

Первым делом преобразуем дробь. Заменим десятичную. на обыкновенную.

\[0,75 = \frac{75}{100}\], \[1,5=\frac{15}{10}\]

Затем проводим сокращение дробных значений и выделяем, по уже изученным правилам целую часть.

\[\frac{125}{1000}\] можно преобразовать и получить следующую дробь 1,125.

Ответ: 1,125.

Пример №2:

Определить произведение чисел \[5,382 \cdot 0,2\].

Первое значение является бесконечной дробью. Ее рекомендуется округлить до сотых значений. Получается \[5,382 \approx 5,38\].

Второй множитель округлять не требуется, это не имеет смысла.

\[5,38 \cdot 0,2=\frac{\frac{538}{100} \cdot 2}{10}=\frac{1,076}{1000}=1,076\]

Следовательно, получаем ответ к нашей задаче: 1,076.

Пример №3:

Необходимо перемножить две периодические дроби. \[0,(3) \cdot 2,(36)\]

Преобразуем заданные значения в обыкновенную дробь.

\[0,(3)=0,3+0,03+0,003+0,003+\ldots=\frac{0.3}{1-0,1}=\frac{0.3}{9}=\frac{3}{9}=\frac{1}{3}\]

\[2,(36)=2+(0,36+0,0036+\ldots)=2+\frac{0,36}{1-0,01}=2+\frac{36}{99}=2+\frac{4}{11}=\frac{2 \cdot 4}{11} \frac{26}{11}\]

\[\Rightarrow 0,(3) \cdot 2,(36)=\frac{\frac{1}{3} \cdot 26}{11}=\frac{26}{33}\]

Полученную в конечном итоге обыкновенную дробь приводим к десятичной. В столбик разделим числитель на знаменатель.

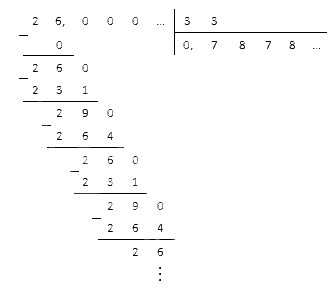
Окончательный ответ : \[0,(3) \cdot 2,(36)=0,(78)\]

Умножение десятичных дробей при помощи столбика

Перемножение столбиком выполняя на условии, что на запятые никакого внимания не уделяется (они игнорируются)

В итоговом результате ставится знак запятой справа. Отделяется столько запятых, сколько множители имеют десятичных знаков вместе.

Если не хватает цифр, то принято в окончательном ответе дописывать нули.

Рассмотрим примеры решения подобных задач.

Пример №1:

Нужно найти значение произведения, следующих чисел: 63,37 и 0,12.

Выполняем умножение, не обращая внимание на запятые.

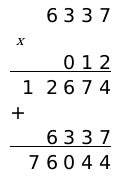
Далее определяемся с запятой, где ее ставить.Она будет через четыре цифры справа. Потому что сумма десятичных знаков двух множителей равна 4.

Нули в данной ситуации не записываются. Это связано с достаточным количеством чисел.

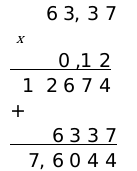
Получаем окончательное значение равное 7,6044.

Пример №2:

Заданные числовые, дробные выражения 3,2601 и 0,0254. необходимо перемножить между собой.

Для этого применим умножение столбиком.

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны. Потому что заданные дроби, вместе, имеют восемь знаков после запятой.

Нули в данной ситуации записываются. Это связано с недостаточным количеством значений.

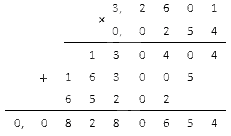
Получаем окончательное значение равное: 0 , 08280654

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Умножение десятичной дроби с обыкновенной и со смешанной дробью

Чтобы произвести данную операцию, необходимо выполнить следующие требования:

Десятичную дробь преобразовывают в обыкновенную и перемножаем с нужным числом.
В десятичную переводим обыкновенную или смешанную дробь и далее перемножаем друг с другом.

Пример 1. Найти произведение \[\frac{3}{5} \text { на 0,9 }\].

Поэтапный процесс решения.

Записываем 0,9 в виде обыкновенной дроби, а именно \[0,9=\frac{9}{10}\].
Перемножаем цифры по правилам математики.
\[\frac{\frac{3}{5}\cdot 9}{10}=\frac{27}{50}=0,54\]
Ответ: \[\frac{3}{5} \cdot 0,9=0,54\]

Пример 2. Найти произведение чисел \[0,18 \text { на } 3 \frac{1}{4}\].

Выполняем следующие действия:

Записываем \[3 \frac{1}{4}\] в виде десятичной дроби:
\[3 \frac{1}{4}=3,25\].
Вычисляем известные нам значения:
0,18 * 3,25 = 0,585.

Ответ: \[0,18 \quad 3 \frac{1}{4}=0,585\].

Пример 3:

Даны следующие значения \[0,4 \text { и } 3 \frac{3}{5} \text {. }\] По условию задач нужно найти их произведение, иными словами перемножить.

Первым делом 0,4 переведем в десятичную дробь и получим значение: \[0,4=\frac{4}{10}=\frac{2}{5}\]

Затем проводим вычисление:

\[0,4 \quad 3 \frac{3}{5}=\frac{\frac{2}{5} \cdot 23}{6}=\frac{23}{15}=1 \frac{8}{15}\]

Полученный ответ является смешанным значением. Его необходимо перевести в значение периодической дроби. А именно: 1,5(3).

Следовательно, это и ответ задачи. 1,5(3).

Возведение в степень дробного числового выражения

Свойство произведения в степень в виде дроби

\[\frac{\left(z^{*} a\right)^{m}}{n}=\frac{z^{m}}{n} \cdot \frac{a^{m}}{n}, \text { при условии что: } \mathrm{z}>0, \mathrm{a}>0, \frac{m}{n}>0\]

В случае если в знаменателе дроби, имеется степень, то ее можно переместить в числитель и при этом необходимо поменять знак на противоположный.

При этом само значение выражения не поменяется.

Данный метод иногда используется при упрощении выражений.

Рассмотрим основные примеры:

Пример 1:

\[\frac{4^{2}}{4^{2}}=1\] — это выражение является верным, так как после преобразования степеней мы получаем \[4^{0}\]. А как гласят правила алгебры — любое число в нулевой степени равно единице.

Пример 2. Перемещение значения степени из знаменателя дробного выражения \[\frac{1}{z^{2} x}\] в числитель

\[\frac{1}{z^{2} x}=z^{-2} x z^{-1}\]

Пример 3. Записать произведение 3x*(x + y)⁻⁴ в виде дроби, которая не имеет степени с отрицательным значением.

Выражение имеет множители 3 и (x + y)⁻⁴. Множитель 3 не изменяем, а множители (x + y)⁻⁴ заменяем на соответственно равную ему дробь \[\frac{1}{(x+y)-4}\]

\[3 *(x+y)-^{4}=3 x \frac{1}{(x+y)-4}\]

Затем перемножим множитель 3 с числителем дроби \[\frac{1}{(x+y)-4}\].

В результате образуется дробь \[\frac{3}{}\]

Итоговый результат: \[3(x+y)-^{4}=3 x \frac{1}{(x+y)-4}=\frac{3}{(x+y)-4}\]

Преобразование дробных значений 0,1, 0,01, 0,001, где основанием степени является число 10

Если степень представлена числами 0,1; 0,01; 0,001 и основание имеет значение 10. Для преобразования необходимо:

указать отрицательный показатель степени;
записать основание равным десяти.

Пример 1: Значение 0,01, где основание — число 10.

В числе 0,01 имеется два 0. Значит, оно будет представлено как 10 ^-2. Значение показателя равно значению нулей в числе 0,01.

0,01 = 10^-2

Число 0,01 это значение деления 1/100, или 1/10²

Пример 2: Значение 0,00001 в виде степени с основанием 10.

0,00001 = 10^-5

Правила деления дробей

Выполнение деления дробных значений по своей аналогии одинаково с умножением.

При делении первую дробь необходимо перемножить со значениями дроби под номером два.

Пример 1:

Дробное значение следующего вида: \[\frac{\sqrt{\sqrt{x+2 \cdot x}}}{x^{2} \cdot\left(\operatorname{Ln} x^{2} \cdot \operatorname{Ln} x+1\right)}\] необходимо разделить на следующую дробь \[\frac{3 \cdot x^{2.3} \cdot(\sqrt{x+1})-2}{\sin (2 \cdot x-\sqrt{x})}\]

Преобразовывая значения можно записать следующую форму:

\[\frac{\sqrt{\sqrt{x+2 \cdot x}}}{x^{2} \cdot\left(\operatorname{Ln} x^{2} \cdot \operatorname{Ln} x+1\right)} / \frac{3 \cdot x^{2.3} \cdot(\sqrt{x+1})-2}{\sin (2 \cdot x-\sqrt{x})}\]

затем заменить произведением следующего вида

\[\frac{\sqrt{\sqrt{x+2 \cdot x}}}{x^{2} \cdot\left(\operatorname{Ln} x^{2} \cdot \operatorname{Ln} x+1\right)} * \frac{3 \cdot x^{2.3} \cdot(\sqrt{x+1})-2}{\sin (2 \cdot x-\sqrt{x})}\]

Приведение дробей к наименьшему общему знаменателю

Наименьший общий знаменатель дробей

Определение

Общий знаменатель значения — это любое из положительных данных числа, которое является кратным для всех значений дробей.

Иными словами, можно сказать, что общим знаменателем дроби, будет характеризоваться натуральное простое числовое значение. Оно должно делиться без остатка на все значения знаменателей данных дробей.

Натуральные числа имеют свойство бесконечности и поэтому ряд обыкновенных дробных значений имеет характерное множество общих значений знаменателя. Чтобы определить общий знаменатель для дроби, нужно применить его основное определение.

Рассмотри два значения дробных выражений: 16 и 35. Общим дробным знаменателем будет являться любое число с положительным значением. Оно должно быть кратным значениям 6 и 5.

Перечислим подходящие значения: 30,35,65,95,125,155,185,215 и так далее.

Данное определение звучит следующим образом: минимальное значение числа, на которое можно разделить знаменатель дроби, обязательно без остаточного значения.

Аббревиатура данного значения, выглядит как НОК.

В определенном перечне числовых значений, которые являются общими знаменателями данных дробей, будет иметь место наименьшее простое значение. Оно будет характеризоваться, как наименьший общий знаменатель. Сформулируем определение наименьшего общего знаменателя данных дробей.

Как правильно определить наименьший общий знаменатель числа дроби?

Так как НОК, будет иметь значение наименьшего положительного общего делителя данного набора чисел. Тогда НОК знаменателей любых дробей, представлен, как минимальный общий знаменатель дроби.

Из этого следует, что определение наименьшего знаменателя дроби, будет сводиться к определению НОК знаменателя дроби.

Рассмотрим данное правило на примере решения.

Пример 1:

Задано два значения дроби: \[\frac{3}{10} и \frac{277}{28}\]

Знаменатели дробей равняются 10 и 28 соответственно.

Наименьший знаменатель будет определяться как НОК чисел 10 и 28.

Разложим числа на простые множители: 10=2*5, 28=2*2*7, следовательно НОК (15 и 28)=2*2*5*7=140.

Ответ задачи: 140

Когда простые обыкновенные дроби, имеют одинаковые по значению знаменатели, то это характеризуется как дроби приведены к общему знаменателю.

Пример 2: значения \[\frac{45}{76} \text { и } \frac{143}{76}\] приведены к общему знаменателю, числу 76. Рассмотрим еще несколько дробей \[\frac{1}{3}, \frac{3}{3}, \frac{17}{3} \text { и } \frac{1000}{3}\] все эти значения приведены к общему знаменателю 3.

В случае, если знаменатели дробных чисел, являются разными по значениям и не равны друг другу. Можно их привести к общему числовому знаменателю. Для этого значение числителя и знаменателя данных значений перемножим с дополнительным множителем.

Например 3: \[\frac{2}{5} и \frac{7}{4}\] — эти дроби имеют разные знаменатели, поэтому воспользуемся приведение к общему знаменателю, при помощи дополнительных множителей, а именно 4 и 5.

Применяя данные значения приведем и вычисления и получим общий множитель: значение равное 20.

При перемножении числителя и знаменателя дроби \[\frac{2}{5}\] на значение равное 4, получим дробь вида \[\frac{8}{20}\]. Проводим аналогичные действия, но только с дробью.

При перемножении числителя и знаменателя дроби \[\frac{7}{4}\] на 5 и приведем ее к дроби вида \[\frac{35}{20}\].

Теперь можно сформулировать определение, приведение дробей к общему знаменателю.

Определение

Приведение дробей к знаменателю одинаковых значений – это вычислительный процесс, который включает в себя: умножение числителей и знаменателей любых значений дробей на определенные значения дополнительных множителей, чтобы результаты проведенных вычислений получились дроби с одинаковыми знаменателями.

В математике существует правило, которое помогает привести дроби к общему наименьшему знаменателю.

Данное правило включает в себя три основных пункта.

Принцип приведения дробного значения к наименьшему общему знаменателю:

Для начала определяется значение наименьшего общего знаменателя дробей.
Затем для каждой дроби определяется дополнительный множитель. Он должен соответствовать правилу: деление наименьшего общего знаменателя на знаменатель, каждой рассматриваемой при решении, дроби.
Перемножаем числитель и знаменатель на принятый дополнительный множитель.

Решение задач с приведением к наименьшему знаменателю

Пример 1:

Нужно привести к наименьшему знаменателю следующие дроби:

\[\frac{5}{14} и \frac{7}{18}\]

Для решения применим алгоритм решения, рассмотренный вышеприведенном пункте.

Для начала определим наименьшее значение общего знаменателя, который равен минимальному и кратному числу 14 и 18.

Разложим значения знаменателей на множители: 14=2*7, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=126.

Следующим шагом, будет вычисление дополнительных множителей. С их помощью приведем дробные значения \[\frac{5}{14}\] и \[\frac{7}{18}\] будут приведены к числу 126.

Дробному значению \[\frac{5}{14}\] дополнительный множитель будет равняться 12614=9. Для значения второй дроби равной \[\frac{7}{18}\] , аналогичный множитель будет равняться 12918=7.

Числители и знаменатели дробей перемножаем на дополнительный множитель 9 и 7 соответственно.

Записываем следующие выражения:

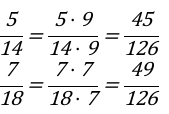
Итоги проведенных вычислений: Заданные дроби \[\frac{5}{14} и \frac{7}{18}\] приведены к общему знаменателю. Итоговое значение выражения \[\frac{45}{126} и \frac{49}{126}\].

Пример 2:

Нужно привести к наименьшему знаменателю следующие дроби:

\[\frac{3}{12} и \frac{5}{18}\]

В этом примере, также применим алгоритм решения, состоящий из трех главным действий.

Используя алгоритм решения, определим наименьшее значение общего знаменателя, который равен самому минимальному значению и кратному числам 12 и 18.

Следующим шагом, разлом данные значения на множители: 12=2*6, 18=2*3*3, следовательно, значение НОК будет равно 2*3*3*7=216.

Произведем вычисление дополнительных множителей. С их помощью приведем дробные значения \[\frac{3}{12}\] и \[\frac{5}{18}\] будут приведены к числу 216.

Дробному значению \[\frac{3}{12}\] дополнительный множитель будет равняться 21612=18. Для значения второй дроби равной \[\frac{7}{18}\], аналогичный множитель будет равняться 21618=12.

Данные значений дробей, нужно перемножить на дополнительный числовой множитель равный числам 9 и 7 соответственно. Подставим эти данные и вычислим составленные выражения.

Записываем следующие выражения:

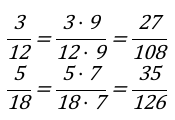
Итоги проведенных вычислений: Заданные дроби \[\frac{5}{14} и \frac{7}{18}\] не приведены к общему знаменателю. Окончательное значение выражения \[\frac{27}{108} и \frac{35}{126}\] и из этого следует, что знаменатели разные.

Ответ: значение 216 не будет являться наименьшим общем знаменателем.

Аналогичным способом, используя алгоритм решения, можно определить значение наименьшего знаменателя трех и более дробных значений.