
Закон сохранения импульса и реактивное движение
Если присмотреться, то действие закона сохранения импульса и энергии можно увидеть в очень многих окружающих нас явлениях. Это удар мяча об стенку, выстрел из пушки, соударение и последующий разлёт различных тел после столкновения. Примеров множество.
Для лучшего понимания темы рассмотрим её в несколько этапов, двигаясь от простого к сложному.
Замкнутая система взаимодействующих тел
Прежде чем начать рассмотрение закона сохранения импульса нужно разобраться с тем, что такое замкнутая система.
Замкнутая система есть система тел, на которую со стороны не действуют никакие внешние силы.
Сразу оговоримся, что это абстракция и идеализация. Замкнутой системы в реальности не существует хотя бы потому, что не существует экранирования от гравитационных сил. В частности, к Земле притягивается любой предмет, имеющий массу, каким бы материалом он не был окружён и где бы на её поверхности не находился.
В ряде случаев действие сторонних сил либо очень малы, либо оказывают пренебрежимо малое влияние на рассматриваемое явление по другим причинам. Взгляните, например, на движение бильярдных шаров по ровной поверхности. Она не может быть абсолютно ровной, прогибается под тяжестью шаров, да и сами они под действием собственного веса несколько деформируются, но всем этим чаще всего можно пренебречь.
Импульс тела, закон сохранения импульса
Импульсом тела называют векторную физическую величину, равную произведению его массы на его скорость.
Закон сохранения импульса. Геометрическая сумма принимающих участие во взаимодействии тел замкнутой системы при любых обстоятельствах остаётся неизменной.
Рассмотрим столкновения двух шаров. Пусть масса одного из них равна m1, а другого m2. Шары движутся навстречу друг другу с постоянными скоростями v1 и v2 по прямолинейным траекториям. Импульсы тел в этом случае у нас соответственно будут равны p1 = m1v1 и p2= m2v2. До того, как произошло столкновение наши шары можно изобразить как:
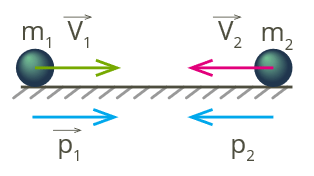
В момент соударения шары будут действовать друг на друга с силами F1 и F2. Именно под их действием изменятся скорости соударяющихся тел. Они станут равными v1, и v2,. Импульсы соответственно приобретут значения p1, и p2,.
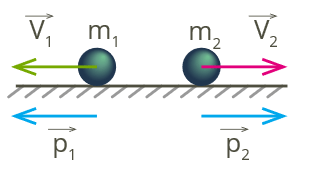
Должно соблюдаться равенство
p1 + p2 = p1, + p2,
С учётом определения импульса его можно написать в виде
m1*v1 + m2*v2 = m1*v1, + m2*v2,
Это есть математическая запись закона сохранения импульса.
Реактивное движение
Реактивным называют такое движение тела, которое возникает при отделении с определённой скоростью некоторой его части. Главные особенности реактивного движения:
- Направление скорости тела всегда противоположно направлению скорости отделившихся его частей. В частности, скорость ракеты по направлению всегда противоположна скорости выброшенных из сопла газов;
- Скорость тела при реактивном движении тем больше, чем больше скорость отделившихся частей и их масса. Чтобы достичь большей скорости ракеты нужно сделать так, чтобы масса истекающих за единицу времени газов или их скорость была как можно больше;
- Полезная масса всегда меньше первоначальной массы реактивно движущегося тела. Для достижения космических скоростей отношение масс составляет около десятка и более раз;
- Одна и та же отделившаяся масса, даже если она всегда отходит от тела с постоянной скоростью, в начале и в конце движения даёт разную скорость разгона. Обусловлено это тем, что масса тела при реактивном движении тела постоянно убывает. В случае ракеты и космических скоростей, убыль достигает очень больших величин.
Основной формулой реактивного движения является формула Циолковского. Чаще всего она записывается в виде:
\[v_{\text {max }}=v_{0}+U^{*} \ln \left(1+m_{t} / m_{k}\right)\]
Где U скорость выброса газов относительно ракеты.
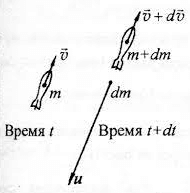
При выводе формулы будем исходить из того, что движение происходит в безвоздушном пространстве и внешние силы (в первую очередь притяжение Земли) равны нулю. В начальный момент времени ракету считаем неподвижной.
Записываем для такой системы закон сохранения импульса при реактивном движении:
m*Δv + Δmv*U = 0
Полная масса системы всегда остаётся постоянной, это означает, что масса выброшенных газов и убыль массы ракеты равны между собой.
Δmv + Δm = 0
Делим m*Δv + Δmv*U = 0 на время и получаем
m(Δv/dt) = U(Δm/dt)
Если перейти к пределу, когда время стремится к нулю, то можно получить соотношение
m(dv/dt) = U(dm/dt)
Т. к. газы из ракеты вытекают в противоположную движению сторону, их скорость будет со знаком минус.
Тогда уравнение запишется
m(dv/dt) = -U(dm/dt)
Если обе части этого равенства умножить на dt и поделить на массу m, то в получится:
-U(dm/m) = dv
Теперь нам нужно проинтегрировать обе части этого уравнения, одну по массе, другую по скорости. Здесь уже нет необходимости считать начальную скорость ракеты равной нулю. Для получения более общего результата так и поступаем.
Интегрирование даст U*ln(m0/m) = v-v0
Далее нам нужно выразить максимальную скорость ракеты. Учитываем, что общая масса ракеты с топливом есть масса собственно ракеты и загруженного в неё топлива, т. е.
m0 = mk + mt
В результате будем иметь vmax = v0 + U*ln[(mk + mt)/mk]
Чтобы выражение было удобнее логарифмировать, лучше его записать в виде
Vmax = v0 + U*ln(1 + mt/mk)
Это и есть итоговая формула Циолковского.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры реактивного движения
В природе реактивным способом движутся многие морские животные, в частности, каракатицы, осьминоги и кальмары. Из растений для своего распространения реактивным движением пользуется так называемый Бешеный огурец. Он может выстреливать семенами на расстояние более 6 м.
Среди примеров реактивного движения для технических устройств отметим эолипил. Он был создан талантливым древнегреческим математиком Героном в 1 веке нашей эры, но практического применения не нашёл.
Другой пример – Сегнерово колесо. Оно представляет собой устройство, реактивная тяга которого стала приносить людям реальную пользу. Конструкция колеса использована в центробежном фильтре очистке масла.
Однако больше всего примеров использования реактивного движения тел можно привести из современной техники. Это реактивные самолёты, реактивные снаряды Град, многоступенчатые ракеты, реактивный водный ранец, и т. д.










