
Формулы сокращенного умножения
Формулы сокращенного умножения (ФСУ) используются для возведения в степень и умножения чисел, выражений. ФСУ помогают производить вычисления быстрее и делают их более компактными.
В нашей статье будут перечислены все необходимые формулы сокращенного умножения, а также, для удобства запоминания, формулы структурируем в таблицу, разберём примеры применения ФСУ, рассмотрим, как сократить формулы сокращенного умножения, наибольшее внимание уделим способам доказательства ФСУ.
Формулы сокращенного умножения (ФСУ): таблица
Тема «Формулы сокращенного умножения» занимает центральное место в школьном курсе алгебры. Математика без формулы сокращенного умножения была бы скучна и сложна. Школьники начинают знакомство с этими формулами в 7 классе курса алгебры. Ниже приведены основные ФСУ формулы сокращенного умножения.
Чтобы с лёгкостью использовать формулы, их нужно заучить наизусть. Сгруппируем их в таблицу и представим ниже, заключив в рамку.
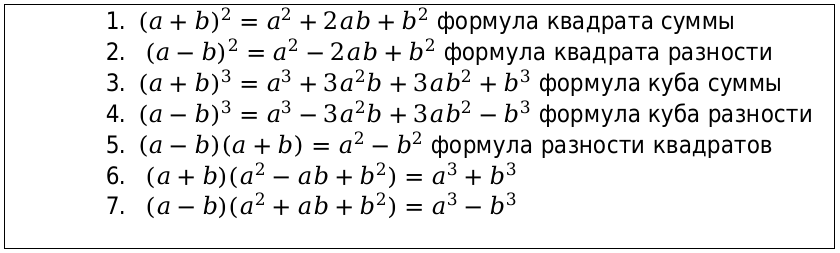
Соответственно, a и b в формулах могут быть заменены на любое число, переменную, выражение.
С помощью первых четырёх формул можно вычислить квадрат, куб суммы и разности 2-х выражений. Формула под номером 5 позволяет вычислить разность квадратов, перемножая сумму и разность выражений.
6-ая и 7-ая формулы вычисляют сумму и разность кубов путём произведения разности и суммы выражений на неполный квадрат разности (суммы).
ФСУ часто синонимично называют тождественные выражения формулы сокращенного умножения. Действительно, левая и правая части этих выражений представляют собой тождества.
Поэтому, решая практические примеры, часто переставляют левые и правые части. Это очень удобно при разложении многочлена на множители.
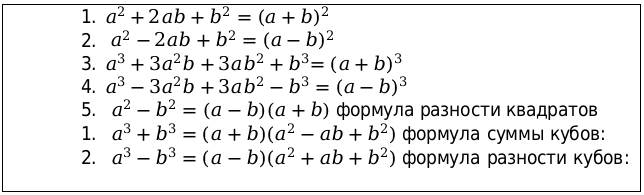
Все необходимые формулы сокращенного умножения по алгебре
Помимо этих формул, выдаваемых на уроках в 7 классе, используются еще несколько формул. Одной из них является бином Ньютона.
В этой формуле \[C_{n}^{n}\] – это биномиальные коэффициенты, которые стоят в строке под номером n в треугольнике Паскаля. Они находятся по следующей формуле:
Треугольник Паскаля – это арифметический треугольник. Он назван в честь Блеза Паскаля. Он состоит из коэффициентов одночленов, входящих в состав формулы степени суммы двух чисел. Если схематично очертить этот треугольник Паскаля, то получим равнобедренный треугольник, у которого по бокам стоят единицы. Каждое нижнее число получается путем сложения двух чисел, стоящих выше него.
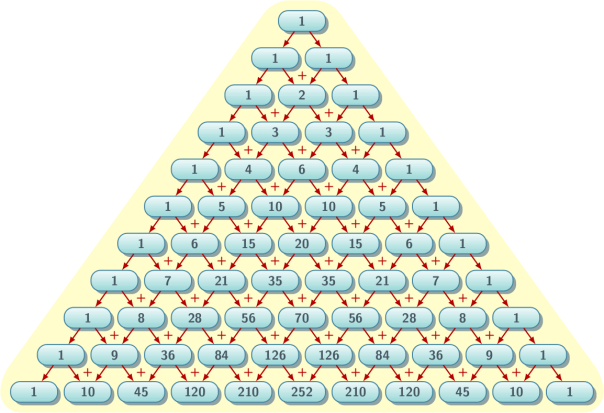
Можно заметить, что формулы сокращенного умножения квадрат(куб) суммы (разности) – это частный случай формулы бинома Ньютона, когда n=2 и n=3.
Если слагаемых больше, чем два, как выполнить возведение в степень? Полезно вывести формулу квадрата суммы слагаемых, больших, чем два.
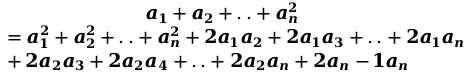
Помимо, запоминания формулы, её нужно научиться правильно читать. Данная выше формула, читается так: «Квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых».
Еще одной нужной формулой в вычислениях является формула разности n-ых степеней 2-х слагаемых.
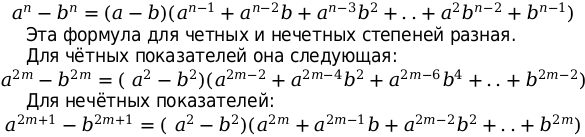
Формулы разности квадратов и разности кубов являются частным случаем формул сокращенного умножения.
Способы чтения формул сокращенного умножения
Прежде чем дать определение всех формул сокращенного умножения, следует пояснить правила формулы сокращенного умножения. Разберём на примере чтение формулы квадрата разности двух чисел.
Квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.
Оставшиеся формулы читаются по такому же принципу.
Квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения. Попробуем прочитать формулу куба суммы: \[(a+b)^{3}=a^{3}+3 a^{2} b+3 a b^{2}+b^{3}\].
Куб суммы двух выражений a и b равен сумме кубов этих выражений, утроенного произведения квадрата первого выражения на второе и утроенного произведения квадрата второго выражения на первое выражение.
Разность кубов \[(a-b)^{3}=a^{3}-3 a^{2} b+3 a b^{2}-b^{3}\] следует читать так: Формула сокращенного умножения куб разности двух выражений a и b равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе, плюс утроенное произведение квадрата второго выражения на первое выражение, минус куб второго выражения.
Пятую формулу следует читать следующим образом: разность квадратов двух выражений равна произведению разности и суммы двух выражений.
называются неполным квадратом суммы и неполным квадратом разности
Зная это, сумма и разность кубов читаются так: сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности. Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.
Доказательство ФСУ
Формулы сокращенного умножения доказываются несложно. Опираясь на свойства умножения, умножим пошагово части формул в скобках.
В качестве примера будем использовать формулу квадрата суммы.
Для того, чтобы возвести выражение во 2-ую степень, это выражение следует умножить само на себя:
Раскрываем скобки:
Что и требовалось доказать.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Примеры использования формул сокращенного умножения
Как уже было сказано, формулы сокращенного умножения позволяют быстро и кратко возвести выражение в степень. ФСУ применяются еще и при сокращении дробей и выражений, разложении многочленов на множители, вычислении интегралов и пределов. Рассмотрим примеры формулы сокращенного умножения. Эти примеры содержат уже готовые формулы сокращенного умножения и ответы.
Пример 1. Преобразовать выражение \[(1+5 x)^{2}-12 x-1\] в многочлен стандартного вида. Раскроем скобки, используя формулу квадрата суммы, и приведем подобные слагаемые. \[(1+5 x)^{2}-12 x-1=1+10 x+25 x^{2}-12 x-1=25 x^{2}-2 x\]
Пример 2. Разложить на множители \[25 x^{4}-m^{10} t^{6}\].
Используем формулу степеней и применим формулу разности квадратов: \[25 x^{4}-m^{10} t^{6}=\left(5 x^{2}\right)^{2}-\left(m^{5} t^{3}\right)^{2}=\left(5 x^{2}-m^{5} t^{3}\right)\left(5 x^{2}+m^{5} t^{3}\right)\]
Пример 3. Сократить дробь, при этом используйте формулы сокращенногоСнимок экрана от 2021-12-14 14-48-10 умножения \[\frac{x^{2}-9}{x-3}=\frac{x^{2}-3^{2}}{x-3}=\frac{(x+3)(x-3)}{x-3}=x+3\]
Заметим, что выражение, представленное в числителе, является разностью квадратов формул сокращенного умножения. Применим её и сократим на идентичные выражения в числителе и знаменателе (х-3):
Пример 4. Упростить выражение \[(2 a-3)^{2}-4\left(a^{2}-a\right)\] и найти его значение при \[a=\frac{17}{8}\]
Раскрываем скобки: \[(2 a-3)^{2}-4\left(a^{2}-a\right)=4 a^{2}-12 a+9-4 a^{2}+4 a=-8 a+9\]
Теперь можно подставить в выражение значение переменной а.
Пример 5. Вычислить \[63 \cdot 53\]
Числа 63 и 57 можно представить в виде суммы и разности двух одинаковых чисел. Следовательно, для вычисления произведения \[63 \cdot 57\] удобно использовать формулу разности квадратов. Данное вычисление можно посчитать устно.
Пример 6. Раскрыть скобки \[(5 x-6 y)^{2}(5 x-6 y)^{2}\]
Возведем в квадрат.
Практическое применение формул сокращенно умножения, особенности преподавания в школе
В современной системе образования преобладает системно-деятельностный подход. Это означает, что инициатива к поглощению знаний должна исходить от ученика, а учителю следует только направлять его в нужном направлении. У многих учащихся отсутствует интерес к учёбе, они ссылаются на то, что эти знания нигде не пригодятся в жизни. Как быть учителю в данной ситуации? Какие способы мотивации изучения формул сокращенного умножения найти? Эти замечательные формулы еще как пригодятся в житейских ситуациях. В частности, при подборе строительного материала для дома. Например, вы пришли в супермаркет, и продавец по размеру пола (106 м) навязывает 13 000 м2 паркетной доски. Зная ФСУ, вы с лёгкостью в уме сможете проверить, не обманывает ли вас работник магазина.
(106 м)2=(100+6) 2=10 000+2*100*6+36= 11236 м2
Оказывается, вам достаточно будет 11236 м2.
Многие учащиеся ссылаются еще и на то, что сложно выучить и запомнить все эти семь формул. Если, вы умеете перемножать выражения, то ничего заучивать и не придётся. Известно, что а3=а*а*а. то есть, нужно умножить число или выражение само на себя столько раз, сколько написано в показателе степени.
Рассмотрим выведение формулы куб суммы:
И так можно вывести абсолютно любую формулу. Главное, уметь упрощать выражения, умножать, приводить подобные слагаемые. Кроме аналитического доказательства формул сокращенного умножения, имеет место быть еще и геометрический. О нём нельзя не упомянуть на уроках алгебры. Полезно будет дать это задание в качестве домашнего в рамках исследовательской деятельности учащихся.










