
Максимум и минимум функции
Исследование функции в математическом анализе предполагает нахождение экстремумов, которые представляют собой максимальное и минимальное значение на заданном множестве. Для того чтобы определить минимум функции, необходимо произвести несколько простых операций с ее производной. Сначала следует приравнять функцию к нулю и найти значения переменной, а затем, используя их, разбить координатную плоскость и определить, какие отрезки будут положительными или отрицательными.
Определение максимума и минимума функции
Минимумом заданной функции \[y=f(x)\] принято называть одну некоторую точку, если в ее окрестности соблюдается неравенство \[y=f(x) \geq f\left(x_{0}\right)\].
Таким образом \[x_{0}\] – это и есть минимум.
\[x_{0}\] можно назвать максимумом \[y=f(x)\], если в некоторой ее окрестности будет выполняться следующее неравенство \[y=f(x) \leq f\left(x_{0}\right)\]. В этом случае \[x_{0}\] – будет максимумом.
Максимальные и минимальные участки параболы показаны на рисунке:
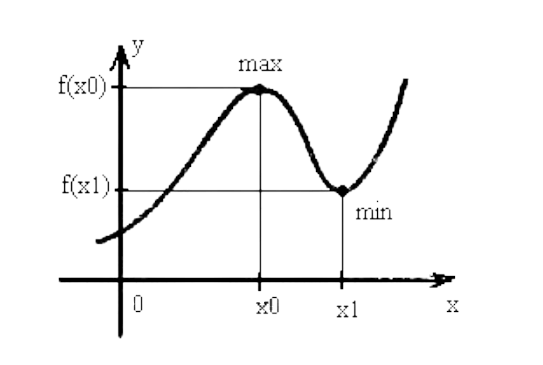
Функция \[y=a x^{2}+b x+c\], имеющая вид параболы, на области определения имеет:
- максимум, при условии, что \[0>a\];
- минимум, при условии \[a>0\].
Экстремум на всей области определения будет совпадать с вершиной параболы. Это показано на рисунке:
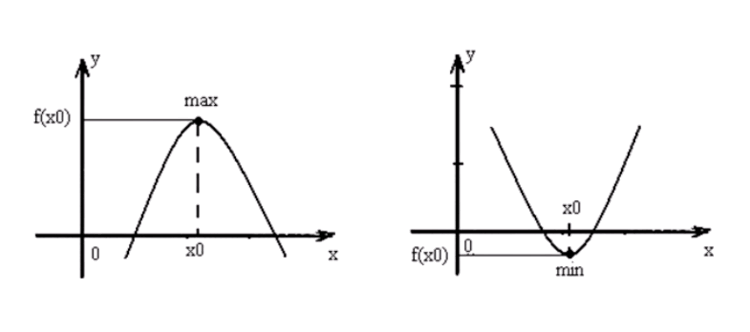
Экстремумы в математическом анализе делятся на два вида:
- глобальный;
- локальный.
К локальному применимо общее определение экстремума. Глобальный вид – это набольшее и наименьшее значение функции на определенном участке.

Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Достижение глобальных экстремумов возможно на обоих концах отрезка, а также в местах нахождения локального экстремума. Для определения их необходимого условия используется следующая теорема:
Если экстремум \[y=f(x)\] находится в некоторой точке \[x_{0}\], то производная \[f^{\prime}(x)\] в той же точке будет равна нулю, либо вовсе не будет существовать.
Для описания достаточных условий экстремума используются следующие теоремы.
Рассмотрим первое условие.
Пусть для \[y=f(x)\] выполняются несколько разных условий:
- \[y=f(x)\] является непрерывной в окрестностях \[x_{0}\].
- При \[x=x_{0}\] производная \[f^{\prime}(x)\] равна нулю или не существует.
- При переходе через \[\chi_{0}\] производная \[f^{\prime}(x)\] меняет свой знак на противоположный.
Исходя из вышеперечисленных условий делаем вывод, что в точке \[x=x_{0}\] будет находиться экстремум \[y=f(x)\].
Если при переходе слева направо через \[x_{0}\] поменяется знак производной с минуса не плюс, то \[x_{0}\] будет являться максимумом функции, если наоборот – то ее минимумом.
Рассмотрим второе условие.
Пусть для функции \[y=f(x) y=f(x)\] выполняются следующие три условия:
- \[y=f(x)\] в окрестностях \[x_{0}\] – непрерывна.
- При \[x=x_{0}\] производная \[f^{\prime}(x)\] равна нулю.
- При \[x=x_{0}\] вторая производная \[f^{\prime \prime}(x)\] не равна нулю.
Следовательно, в точке \[x=x_{0}\] исследуемая функция будет иметь экстремум. Если будет выполнено условие \[f^{\prime \prime}(x)>0\] при \[x=x_{0}\], то можем сделать вывод, что в этом месте находится минимум \[y=f(x)\].
Следует отметить, что если \[f^{\prime \prime}(x)\] не меняет знак при переходе в \[x_{0}\], то в ней не может быть экстремума.
Исследование производится по алгоритму, который включает в себя следующие этапы:
- Нахождение производной \[f^{\prime}(x)\].
- Определение стационарных и критических точек, в которых производная будет равно нулю или вовсе не будет существовать.
- Исследование знака \[f^{\prime}(x)\] на отдельных промежутках с использованием числовой прямой.
- Нахождение экстремумов.
- Определение значения исследуемой функции.
Нужно исследовать \[y=2 x^{3}+12\] на максимум и минимум.
Решение: Решение задачи следует начать с нахождения производной \[y^{\prime}=\left(2 x^{3}+12\right)=6 x^{2}\]. Далее потребуется определить стационарные и критические точки \[y^{\prime}(x)=0 ; 6 x^{2}=0 ; x=0\].
Для исследования знака \[f^{\prime}(x)\] используем стандартную числовую прямую. Наносим на нее интересующую нас точку и находим знак производной слева и справа от нее. Для этого потребуется из каждого промежутка взять произвольное значение и определить значение производной. После этого на числовой прямой определяем знак полученной величины.
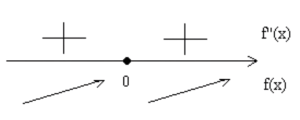
Поскольку производная не меняет свой знак при переходе через критическую точку, можно сделать вывод, что в ней нет экстремумов.
График представлен на рисунке:
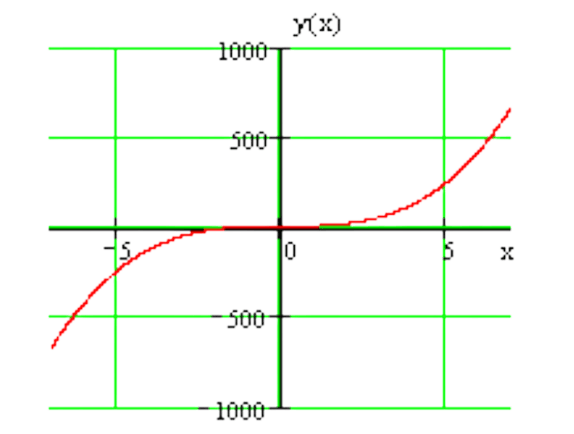
Необходимо исследовать заданную функцию \[y=2 x^{2}+12 x\] на максимум и минимум.
Решение:
Для того чтобы решить эту задачу, сначала нужно найти производную \[y^{\prime}=\left(2 x^{2}+12 x\right)=4 x+12\]
Далее следует определить критические и стационарные точки: \[y^{\prime}(x)=0: 4 x+12=0 ; x=-3\].
На завершающем этапе требуется определить знак с использованием числовой прямой:
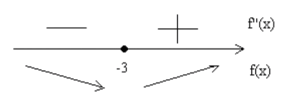
Делаем вывод, что точка минимума \[x=-3\]
\[y(-3)=2 *(-3)^{2}+12 *(-3)=2 * 9-36=-18\]
График \[y=2 x^{2}+12 x\] представлен на рисунке:
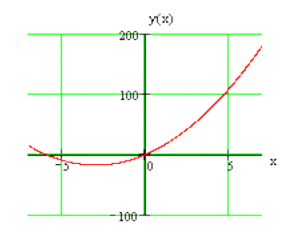
Рассмотренные примеры наглядно показывают, как должно осуществляться исследование функции в математическом анализе. Однако следует учитывать, что в процессе выполнения любого задания нужно также обращать внимание на точки разрыва и интервалы, которые входят в непосредственную область определения. Бывают такие случаи, когда производная находится именно на этих участках.










